(Note: I also created an interactive version of this post in the Desmos Activity Builder. Try it here.)

Hey y’all!

I want to tell you a story today about racism and mathematics.

Well, to be more specific, I’m going to make the argument that trends in mathematical notation can have culturally biased consequences that conferred systematic advantages to white people. I’m going to make this argument through a sequence of math problems, so I hope you’ll follow along and attempt them.

I don’t know if I’ll be able to “prove” this argument to you in the course of this activity, but hope this activity at least instills a sense of “doubt” in the idea that math is objectively neutral.

Without further ado, let’s get started.

Place a mark on the number line where you think “1 Thousand” should go.

Got it?

Okay, I’m going to make a guess as to where you placed it.

Ready?

Did you place it at point P below?

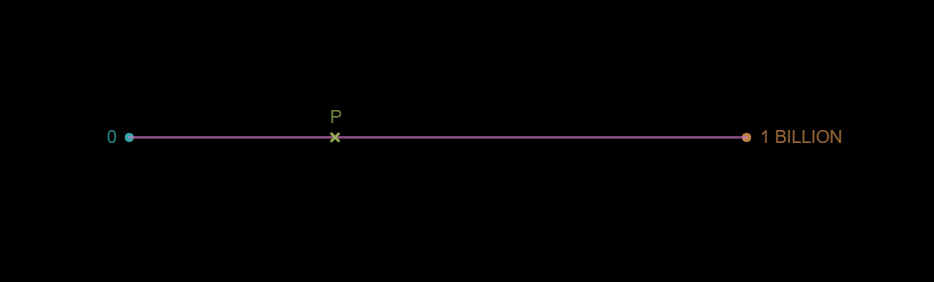
Sorry, I hate to be the one to break it to you, but according to the ‘math powers that be’, this is technically incorrect. However, I want you to hold onto this idea because I’d argue that you’re not as wrong about this as they say you are.

Here’s where you “should” have placed it.

When mathematicians present you with a graph, we implicitly assume that the graph is on a “linear scale”. That means that each unit is equally spaced along the line.

One billion divided by one thousand is one million, which means that “1 thousand” should be placed “1 millionth” of the way between 0 and 1 billion.

At the scale of this graph, this number is so close to the 0 that they’re visually indistinct.

So what about that other point?

That’s actually placed at the value 1/3*10^9 or “one third of a billion”.

However, I don’t want you to think you’re wrong if you placed it here. In fact, this is the correct placement of 1000 on another type of scale.

Check out the following scale instead:

So what would you call a scale like this?

Take a second and write it down.

Go ahead. I’ll wait.

According to the “mathematical community”, this is called a “logarithmic scale”.

Under a logarithmic scale, each successive “unit” gets multiplied by a common factor, such as 10, rather than adding. This results in a scale like in the diagram, only the “0” is actually 10^0 = 1.

There’s even research suggesting that human may actually be predisposed to think of numbers this way, and that the linear scale is a learned behavior. We see it in Indigenous cultures, in children, and even other species. Thinking “linearly” is a social norm that is distributed through cultural indoctrination. It’s like mathematical colonialism.

Here’s my problem with that diagram. If I hadn’t been taught to call this a “logarithmic scale”, I would have called it a “power scale” or an “exponential scale”. Doesn’t that name intuitively make more sense when you see this sequence of labels?

Before we go any further, let’s talk about mathematical notation.

What do you think makes for “good mathematical notation”?

What sort of patterns do you see in the ways that mathematicians name things the way they do?

Here’s what I perceive as the primary patterns in mathematical notation.

Mathematicians sometimes name things “descriptively”: the name tells you what the thing is. For example, the “triangle sum theorem” tells you implicitly that you’re going to add up three angles.

Mathematicians sometimes name things “attributively”: the name tells you who came up with the idea. For example, “Boolean Algebra” is named after “George Boole”.

Mathematicians sometimes name things “analogously”: using symbols with visual similarities to convey structural similarities. For example, “∧ is to ∨ as ∩ is to ∪”.

Mathematicians sometimes name things completely “arbitrarily” for historical reasons. Don’t even get me started on the “Pythagorean Theorem”…

Where would you classify “logarithm” in this scheme?

Personally, I think it depends on who you ask.

If you know a little Greek (which is a cultural bias in itself), you might argue that this label is “descriptive”. The word “logarithm” basically translates to “ratio-number”. The numbers in this sequence are arguably in “ratios” of 10, but does that actually convey enough information for you to know what logarithms really are?

I’d argue that this label is in fact “arbitrary” and actually refers to “how logarithms were used” rather than “what logarithms are”.

So what is a logarithm?

Generally speaking, we define a “logarithm” as the “inverse power function” or “inverse exponential function”.

Just as subtraction undoes addition, and division undoes multiplication, a logarithm undoes a power.

For example, 10^5 = 10000 so log₁₀(10000) = 5.

Though a little clumsy, maybe this will make way more sense if we just used the following notation:

log₁₀(10000) = power?₁₀(10000) = 5

The natural inverse of “raising something to a power” would be “lowering it” it right? The mathematical statement, log₁₀(10000) says this:

“What power of 10 will give you the number 10000?”

The answer to that question is 5. This is the essence of a logarithm.

So why don’t we just call logarithms “inverse exponents”?

Well, we call them “logarithms” because this was the term popularized by a guy named John Napier in the early 1600s.

Normally I’d be okay with the guy who created something getting to name it. However, I don’t think that honor should necessarily go to Napier. This idea of “inverse powers” had shown up in the early 800s thanks to an Indian mathematician named Virasena, and the way Napier employed logarithms was similar to an ancient Babylonian method devised even earlier than that.

What Napier did, in my opinion, was convince other white folx of the power inherent in logarithms.

Please, allow me to demonstrate with some “simple” arithmetic. Try to do these two problems without a calculator.

Problem A: 25.2 * 32.7

Problem B: 1.401+1.515

Go head, take as much time as you need.

Which problem was harder?

Problem A, right?

Here’s the mathematical brilliance of the logarithm. It turns out that this “inverse power function” can be used to take a very difficult multiplication problem and turn it into a much simpler addition problem. Problems B can be used to provide a very reasonable approximation to Problem A in a fraction of the time if you look at it through the use of logarithms. They didn’t have computers back then, so they used tables of precalculated logarithms to drastically speed up the computation of large products.

Here’s how it works.

Start by looking up the logarithms of the numbers you want to multiply:

log(25.2) ≈ 1.401

log(32.7) ≈ 1.515

Once you’ve taken the logs, add them together.

1.401+1.515 = 2.916

Finally, do a reverse look up to find the number that would produce this logarithm.

log( ? ) = 2.916 = log( 824.1 )

This reverse look-up is really the power function: 10^2.916 ≈ 824.1.

Pretty neat?

The result 824.1 is pretty darn close to the actual value of 824.04. It’s not perfect because we rounded, but it’s reasonable enough for many applications.

This idea of using logarithms to speed up calculation resulted in the invention of the “slide rule”, a device which revolutionized the world of mathematics. Well, more accurately, it revolutionized European mathematics at approximately the same time that the British Empire just happened to start colonizing the globe.

Let’s spell that timeline out a little more explicitly:

~800 CE: Indian mathematician Virasena works on this idea of “inverse powers”.

~1600 CE: John Napier rebrands this idea as a ‘logarithm’.

~1700 CE: Invention of “slide rule” using logarithms to speed up calculations helps turn Europe into an economic powerhouse.

~1800 CE: The British Empire begins colonizing India.

Do you think this is a coincidence?

I don’t.

I think European mathematicians were quite aware of the power this tool provided them. Naming this tool a “logarithm” was a way of intentionally segregating mathematical literature to prevent other cultures from understanding what logarithms really are.

When a tool provides this much computational power, the people using that tool have a strong motivation to keep that power to themselves.

It’s like the recent linguistic shift in the usage of “literally” and “figuratively”. People have used the word “literally” to describe things “figuratively” in such large numbers that they have literally changed the meaning of the word.

Logarithms have been used to describe exponential behaviors for so long that the relationship between “powers” and “inverse powers” has become blurred by mathematical convention.

This has far reaching consequences for mathematics education where we need students to understand the implications of exponential growth. This is even more important considering the recent COVID-19 pandemic.

Consider the following example from the New York Times:

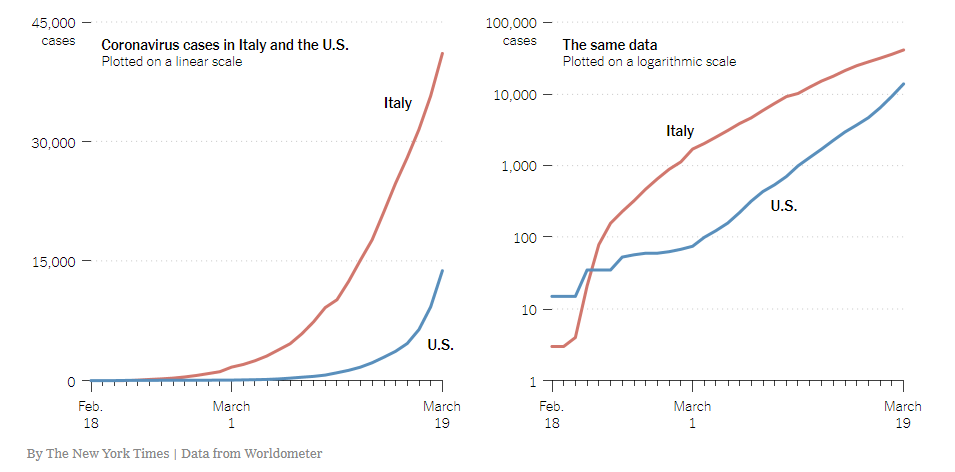
If I accidentally referred to the second graph as an “exponential scale” instead of “logarithmic scale”, would you still know what I was talking about?

What’s the point of calling it that?

I think we need to acknowledge that there exist “self-reinforcing power structures” in mathematics. These mathematical tools provide power to people, so those people fight to keep that power to themselves. This is an act of “segregation”.

After time, these tools become unavoidably common place. Now we’re in a situation where mathematicians argue that these norms should be “assimilated” because their use has become so widespread.

As a result, these cultural biases have resulted in a sort of mathematical colonialism that masquerades as objectivity. I believe that this ethnocentrism systematically disenfranchises BIPOC by hiding the true history of these mathematical ideas. This, in turn, results in systematic biases in test scores between whites and BIPOC, which then reinforce the original stereotypes.

It’s a vicious cycle of racism.

Wouldn’t you agree?

It might be too late to stop the use of the word “logarithm” in mathematics. It’s now something of a necessity to understand a wealth of other mathematical advances that have been built on top of this concept. However, that doesn’t mean we should pretend that this term is completely neutral either.

I hope you’ll leave here today with a better understanding of why it’s important to look critically at our mathematical conventions and acknowledge that math is not exempt from cultural biases.

Thanks for reading!