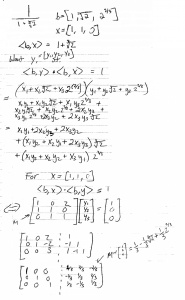This week’s topic on #mathchat was “What books would you recommend for mathematics and/or teachers, why?”. I offered several suggestions in Thursday’s chat, but wanted to go back and explain in more detail “why”. I’ve also added a few to help round out the selection. These books are listed in approximate order of “increasing density”, with the more casual titles at the top and the more math intensive titles near the bottom. Of course, this ordering is my own subjective opinion and should be taken with a grain of salt.

Disclaimer: The author bears no connection to any of the publications listed here, nor was the author compensated for these reviews in any way.

Lewis Carroll – “Alice’s Adventures in Wonderland”, “Through the Looking-Glass”

Recommended for: all ages, casual readers

Charles Dodgson, perhaps better known by his pen-name “Lewis Carroll”, authored a number of children’s books including the aforementioned titles. What makes these books so special, is that Dodgson was also a mathematician and embedded numerous mathematical references in these works. Most people might be familiar with the many film adaptations of these works, but I’d highly recommend reading the originals with an eye towards the logical riddles and mathematical puzzles hidden in these classics. You can find these books online at Project Gutenburg. For little a taste of the mathematics involved, you might start here.

Charles Seife – “Proofiness: The Dark Arts of Mathematical Deception”

Recommend for: teens and older, casual readers, who don’t think math is relevant to daily life

This book focuses on what I consider to be a important topic in the current socio-political climate. Ordinary people are repeated bombarded by “deceptive mathematics”. Whether the source is trying to sell a product or push a political agenda, the inclusion of numeric figures or fancy graphs can go a long way to make a claim look more legitimate than it really is. Proofiness spells out some of the common warning signs of deceitful mathematics, so that the reader can be more aware of these practices. While somewhat lighter on the mathematical content that more advanced readers might expect, I think this book sheds some much needed light on an important social issue and was an enjoyable read. If you like this, you may also like How to Lie with Statistics by Darrell Huff

Apostolos Doxiadis, Christos H. Papadimitriou, Alecos Papadatos and Annie Di Donna – Logicomix

Recommended for: casual readers, comic book fans

Technically this is a graphic novel instead of your typical book, but that doesn’t mean it doesn’t cover some important mathematics! Logicomix presents Betrand Russell as the antagonist in a series of historical events that took place in the early 20th century, culminating with Kurt Gödel’s Incompleteness Theorem. which shook the very foundation of mathematics. Logicomix makes superheroes out of mathematicians in an epic story, while exposing the reader to some amazing mathematics. Ties in nicely with Gödel, Escher, Bach below.

David Richardson – “Euler’s Gem”

Recommend for: casual readers curious about topology

I was looking for a casual introduction to topology and found this little “gem”. This is the book that I wish I read while studying topology in college! It covers everything from the basic principles of topology to the recently solved Poincaré Conjecture. Don’t let all this mathematics scare you away from this title! The book is still written in a very approachable manner. It chronicles the life history of Leonard Euler, presenting the development of the field of topology in context that even the casual reader can enjoy.

Douglass Hofstadter – “Gödel, Escher, Bach: An Eternal Golden Braid”

Recommended for: semi-casual readers with diverse interests

When someone asks me for “a good math book”, this is my go-to recommendation. This book has a little of something for everyone. Math, music, art, language, computers, biology, and psychology are woven seamlessly into a humorous and playful narrative, reminiscent of Lewis Carroll. It goes deep into mathematical concepts where appropriate, and uses visual material and metaphor to bring complex concepts down to Earth. I listed it as “semi-casual” due to the depth of mathematics involved, but a casual reader can skip some of the more math intensive parts and still get a nice overview of the general principles.

Jean-Pierre Changeux and Alain Connes – “Conversations on Mind, Matter, and Mathematics”

Recommended for: semi-casual readers, with interest in philosophy

This book spans several conversations between a Mathematician and a Neurologist on the Nature of Mathematics. One of the central questions is if mathematical ideas have an existence of their own, or if they exist only within the neurology of the human brain. Both sides present some fascinating support for their side of the argument. The material can be a little dense at times, making reference to advanced research as if it were common knowledge, and might not be appropriate for more casual readers. However, a reader willing to dig in to these arguments will reveal two very fascinating perspectives on the philosophy of mathematics.

James Gleick – “Chaos: Making a New Science”

Recommended for: semi-casual readers, preferably with some Calculus experience

Chaos takes the reader on a historical journey through the emergence of Chaos Theory as a mathematical field. An amazing journey through the work of numerous mathematicians in different fields, who came upon systems exhibiting “sensitive dependence on initial conditions”. This book serves as an introduction to both Chaos Theory and non-linear dynamics, while shedding light on the process behind the development of this field. Some experience with differential equations would be beneficial to the reader, but more casual readers can get by with assistance of wonderful visual aids. A nice complement to A New Kind of Science below.

Roger Penrose – “The Emperor’s New Mind: Concerning Computers, Minds, and the Laws of Physics”

Recommended for: more advanced readers with interests in physics and artificial intelligence

Roger Penrose is a well established mathematical physicist, and The Emperor’s New Mind offers an accurate and well written overview of quantum physics. However, what makes this book interesting is that Penrose takes this physics and mathematics to mount an attack on what Artificial Intelligence researchers describe as “strong AI”. Penrose makes the case that Gödel’s Incompleteness Theorem implies that cognitive psychology’s information processing model is inherently flawed — that the human mind can not be realistically modeled by a computer. Whether you agree with Penrose’s conclusions or not, his argument is insightful and is something that needs to be addressed as the field of cognitive psychology moves forward.

Stephen Wolfram – “A New Kind of Science”

Recommended for: more advanced readers with interest in computer science

Don’t let its size intimidate you. If you made it through the titles above, than you should be ready to make headway into this giant tome. The central theme of A New Kind of Science is that complex phenomena can emerge from simple systems of rules. This is different from Chaos Theory (described above), in that this complexity can emerge regardless of initial conditions. A New Kind of Science takes the stance that we can learn a great deal about mathematics through experimentation, and makes the case that perhaps the vast complexity of the universe around us can be explained by a few simple rules.

One of many insightful educators I follow on Twitter, Tom Whitby, wrote A Modest Blog Proposal asking for bloggers to post educational suggestions on October 17th, 2010. He proposed the acronym REBELS for “Reforms from Educational Bloggers Links of Educational Suggestions”. I found the idea of a “rebel” education very intriguing and if there’s one place where educators need to resist authority, I think it’s the mathematics curriculum.

Before we get into my proposed curriculum, it’s important to have an idea of where we’re starting. Paul Lockhart describes the existing system quite concisely in A Mathematician’s Lament:

The Standard School Mathematics Curriculum

LOWER SCHOOL MATH. The indoctrination begins. Students learn that mathematics is not something you do, but something that is done to you. Emphasis is placed on sitting still, filling out worksheets, and following directions. Children are expected to master a complex set of algorithms for manipulating Hindi symbols, unrelated to any real desire or curiosity on their part, and regarded only a few centuries ago as too difficult for the average adult. Multiplication tables are stressed, as are parents, teachers, and the kids themselves.

MIDDLE SCHOOL MATH. Students are taught to view mathematics as a set of procedures, akin to religious rites, which are eternal and set in stone. The holy tablets, or “Math Books,” are handed out, and the students learn to address the church elders as “they” (as in “What do they want here? Do they want me to divide?”) Contrived and artificial “word problems” will be introduced in order to make the mindless drudgery of arithmetic seem enjoyable by comparison. Students will be tested on a wide array of unnecessary technical terms, such as ‘whole number’ and ‘proper fraction,’ without the slightest rationale for making such distinctions. Excellent preparation for Algebra I.

ALGEBRA I. So as not to waste valuable time thinking about numbers and their patterns, this course instead focuses on symbols and rules for their manipulation. The smooth narrative thread that leads from ancient Mesopotamian tablet problems to the high art of the Renaissance algebraists is discarded in favor of a disturbingly fractured, post-modern retelling with no characters, plot, or theme. The insistence that all numbers and expressions be put into various standard forms will provide additional confusion as to the meaning of identity and equality. Students must also memorize the quadratic formula for some reason.

GEOMETRY. Isolated from the rest of the curriculum, this course will raise the hopes of students who wish to engage in meaningful mathematical activity, and then dash them. Clumsy and distracting notation will be introduced, and no pains will be spared to make the simple seem complicated. This goal of this course is to eradicate any last remaining vestiges of natural mathematical intuition, in preparation for Algebra II.

ALGEBRA II. The subject of this course is the unmotivated and inappropriate use of coordinate geometry. Conic sections are introduced in a coordinate framework so as to avoid the aesthetic simplicity of cones and their sections. Students will learn to rewrite quadratic forms in a variety of standard formats for no reason whatsoever. Exponential and logarithmic functions are also introduced in Algebra II, despite not being algebraic objects, simply because they have to be stuck in somewhere, apparently. The name of the course is chosen to reinforce the ladder mythology. Why Geometry occurs in between Algebra I and its sequel remains a mystery.

TRIGONOMETRY. Two weeks of content are stretched to semester length by masturbatory definitional runarounds. Truly interesting and beautiful phenomena, such as the way the sides of a triangle depend on its angles, will be given the same emphasis as irrelevant abbreviations and obsolete notational conventions, in order to prevent students from forming any clear idea as to what the subject is about. Students will learn such mnemonic devices as “SohCahToa” and “All Students Take Calculus” in lieu of developing a natural intuitive feeling for orientation and symmetry. The measurement of triangles will be discussed without mention of the transcendental nature of the trigonometric functions, or the consequent linguistic and philosophical problems inherent in making such measurements. Calculator required, so as to further blur these issues.

PRE-CALCULUS. A senseless bouillabaisse of disconnected topics. Mostly a half-baked attempt to introduce late nineteenth-century analytic methods into settings where they are neither necessary nor helpful. Technical definitions of ‘limits’ and ‘continuity’ are presented in order to obscure the intuitively clear notion of smooth change. As the name suggests, this course prepares the student for Calculus, where the final phase in the systematic obfuscation of any natural ideas related to shape and motion will be completed.

CALCULUS. This course will explore the mathematics of motion, and the best ways to bury it under a mountain of unnecessary formalism. Despite being an introduction to both the differential and integral calculus, the simple and profound ideas of Newton and Leibniz will be discarded in favor of the more sophisticated function-based approach developed as a response to various analytic crises which do not really apply in this setting, and which will of course not be mentioned. To be taken again in college, verbatim.

So if Educational Rebels could have their way with the math curriculum, what would it look like instead? Certainly it would be different from what goes on in the Educational Empire.

Rebel vs. Empire terminology geekily borrowed from Star Wars. Image obtained from Wookieepedia.

Within the Educational Empire, there are Official Imperial Standards which teachers must adhere to or they will be fired and annual multiple-choice tests that students must take as if their lives depended on them. As Imperial teachers routinely state, students who do poorly on these tests will die poor and lonely, and students who do well on these tests will go on to an Empire approved Private Academy where they will accumulate massive debts which must be repaid to the Empire through decades of hard labor.

The Rebels would do away with all of this. Instead of multiple-choice choice tests, students would have authentic assessments where they create products they can be proud of. Teachers would have educational goals in mind for instruction, but the nature of the material covered is directed by the students. Students are free to learn about the things they are genuinely interested in, and often go home telling their parents how they “can’t wait to go to school tomorrow”. Upon graduating from public schools, students are well prepared to start pursuing the career of their choice. Those who want to further the field of knowledge in their respective area of interest can go on to to a Rebel college for free, where they are guided in conducting effective scientific research.

The Rebels would need to rewrite the curriculum from scratch to accomplish all of this, starting with the math curriculum. The new curriculum would be nonlinear and individualized for each student. The students would be the ones to direct learning, and the teacher would be there as an experienced learning guide. The following tale describes the math curriculum of some hypothetical Rebel students:

Rebel Mathematics Curriculum

Elementary School

Student exposure to mathematics begins with games. Students start with simple games in the beginning, and the games get more complicated as the students progress. These particular students start with games like Rock-Paper-Scissors, Go Fish, Tic-Tac-Toe, Hide-and-Seek and Dodgeball. In the context of these games, students learn how to play within a set of rules and learn the basic language of logic and sets. Students learn what it means when the rules say “Do this and this”, “Don’t do this or that”, “Move this from this group to that group”, “Combine this group and that group”, “Separate this group into multiple groups based on some quality”. These concepts form a solid foundation for mathematical thinking. As students progress, they get into games where counting becomes more important. Students play games like Sorry!, Chutes and Ladders, Hi Ho Cherry-O, and even sports like Tennis. As students become more familiar with counting, they get into games with more complex scoring methods like Yahtzee, Blackjack, Monopoly, and Risk where they further develop their arithmetic skills.

Dice games like Yahtzee can be used to introduce basic arithmetic skills. Image obtained from Wikipedia.

Middle School

In Middle School, students continue to play increasingly complex games. Students play board games like Chess and Go, card games like Poker, and video games like Sim City and World of Warcraft. Students are encourage to engage in meta-cognitive processes as they play, by talking about different strategies for optimizing how they play. The basic concepts behind Algebra and Probability emerge naturally from these discussions. Students start developing games of their own, beginning with board and card games and moving into programming simple video games. That’s right, all students are encouraged to start programming in middle school. After the students develop a prototype game, they play-test the game, collect data from the play-test, analyze that data, and use the information they discover to revise the rules of their game. The middle school hosts a Game Convention at the end of the school year where each class puts on a demonstration of their game and the process they used to come up with it. The parents are invited to come play their kids’ games and see how the students’ critical thinking skills have developed.

Game record of a Go match between Honinbo Shuusaku and Gennen Inseki in 1846. Image obtained from Wikipedia. The game of Go is immensely complex, and one of few games where Artificial Intelligence research has yet to reach the level of professional human players.

High School

In High School, the class of students that worked as a group in middle school starts to diverge into different groups based on individual interests. Students with an interest in sports might have a math course that is focused on Geometry and Spacial-Reasoning, with a little bit of Game Theory on the side. Students with an interest in Music might combine Trigonometry and a little computer programming to produce new and interesting sound effects. A group of photography and art students start programming new filters in GIMP to create original effects for their images. A group of students interested in journalism learns about web programming as they put together a professional looking web site. A group of students that developed an interest in Racing games, is introduced to physics and some real-world automotive engineering. A group of students with an interest in programming starts learning about Calculus as they write their own First-Person Shooter. Another group of students uses a Lego Mindstorms kit to build a robot that sorts a line of objects by size, learning a variety of math and engineering skills in the process. Students graduate from high school with more than just a diploma, but a portfolio of work demonstrating their mastery in their subject area of interest. Students show off these portfolios at a convention where the local employers are known to stop by to identify potential job candidates. Most of these students will move straight into a job in their field of interest, but some will go on to pursue further research opportunities in college.

Products like Lego Mindstorms can be used in high school to develop practical engineering skills. Image obtained from Official Lego site.

College

All Rebel students have the option of furthering their education in a publicly owned and operated Rebel University. This education is provided at no cost to students. Exceptional students conducting research at the Rebel University may even be paid for their contributions. Rebel society recognizes the value of academic research, and considers the value of the knowledge resulting from student research to more than compensate for the costs associated with running the Rebel University. Students don’t just go to college to learn, they go to further the existing knowledge in their respective fields.

Conclusion

In this Rebel Education, gone are the days of Algebra, Geometry, More Algebra, Trigonometry, and Calculus. Gone are the days of lengthy multiple choice tests. Teachers assess students by analyzing the products they create and encourage the students themselves to critically reflect on their own creations. Students are not pressured to meet Imperial standards, but instead are responsible for setting their own goals for improvement each semester. The students don’t feel like they are competing to score higher than their classmates, but instead learn to recognize that each of their classmates has a different set of skills and that by cooperating they can achieve things that they could not do alone. While the Empire is pumping out clone after clone, the Rebels are producing a diverse array of students with varying sets of knowledge and skills.

Which students do you think would be happier and more successful in life? Those with their Empire prescribed cookie-cutter education? Or those from the Rebel academies?

I must confess that there has not been enough research to predict what the long-term effects of such a Rebel education would be. However, I do think there is a substantial amount of evidence indicating that the traditional Imperial curriculum is failing. Educational research provides incremental improvements to the existing curriculum, but perhaps the system’s assumption that everyone should have the same education is fundamentally flawed. At some point in the future, it may become necessary for “Educational Rebels” to overthrow the “Educational Empire” and challenge this assumption. The mathematics curriculum proposed here may not be perfect, but it might provide a starting point that educators can revise and improve over time.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. You are free to share and remix this work, provided that the source is properly attributed and derivations are released under a similar license.

Over at the Republic of Math, Gary Davis launched a preemptive strike on Thursday’s upcoming #mathchat topic: “Does the nature of mathematics change as students get older or is it only the teaching methods that change?”. His conclusion? Neither. I would tend to agree with this, but I’m going to play devil’s advocate here and argue a different perspective.

Looking at this from the overall historical perspective, the “nature of math” has not changed very much over the years. The concepts at the core of mathematics, like quantities and patterns, are the same as they were thousands of years ago. The teaching methods for encouraging development also remain fundamentally the same as students age. Teachers seek to identify a student’s present level of understanding and design learning activities that will bring that understanding to the “next level”. From this perspective, neither the nature of math nor methods of teaching change over time.

However, there’s something interesting in how this #mathchat topic is phrased. The question is not “does the nature of math change over time?” but rather “does the nature of math change as students get older?”. If we concede the former point about the nature of math remaining the same over time from a historical perspective, the phrasing of the #mathchat topic hints at an alternative interpretation. Redirecting this question to the reader:

Did the “nature of math” change as you got older?

My answer to this is “Yes”. The “nature of math” became more and more refined as I was exposed to new mathematical ideas. In particular, my preconceived notions about “the nature of math” were shattered into pieces when I learned about this guy:

Around the turn of the 20th century, Russell, Whitehead and Hilbert were attempting to build a solid foundation for mathematics using logic and set theory. This is more or less how I thought of the “nature of math” prior to college. I thought that if I only understood the basic rules of the “math game”, I could figure out anything I needed to from applying those rules in a logical manner. It turns out I was wrong.

In 1931, Gödel published his famous Incompleteness Theorem. This result proved that the kind of system that Russell, Whitehead and Hilbert were attempting to create would either be incomplete or inconsistent. Likewise, this theorem single-handedly destroyed the concept of “the nature of math” that I had built up over the years. In its place I started to form a new concept about the “nature of math”. Gödel had taught me to start looking at mathematics from outside the box.

Some other works that altered my notions about the nature of math were Turing’s proof that the Halting Problem is undecidable and Cantor’s Diagonal Argument. There are many parallels between all three of these results. What really resonated with me was the metacognitive component to these proofs. The nature of math had shifted from thinking about how I could play within the rules of the game, to thinking about how those rules could be bent or broken. Instead of “thinking about math”, I started “thinking about how I thought about math”.

This change in my perception of the nature of math not only influenced my future learning, but also changed how I thought about previous topics. The Republic of Math article mentions trigonometry, which is one of those areas that I was forced to revisit with this new perspective. As Gary notes in this and previous posts (here and here), there are lots of problems with trigonometry’s reliance on triangles. Under my new “nature of math”, the assumption that triangles needed to lie in a Euclidean space was no longer a safe assumption to make.

My background as computer programmer also altered my conception of trigonometry. Because trig functions and square roots can be computationally expensive, I developed a habit of avoiding them whenever possible. Most of the time I can get the data I need from a dot product instead of working with angles. Instead of using the distance between points, I’ll often use the square of the distance as my metric. I’d learned to not just solve the problem, but to reflect on how I was solving the problem and try to optimize that process.

This brings me to the second part of the #mathchat prompt, which is “do teaching methods change as students get older?”. Earlier I discussed the notion that the teacher should identify a students level of comprehension and guide them towards the “next level”. With this trigonometry example, we can see that this model is overly simplistic. Math is not linear. Instead, the teacher must not only identify the student’s current conception, but also which path that student is following so they can encourage them in that direction. If students are starting to think about trigonometry in terms of vector dot products, guide them towards linear algebra. If students are starting to think about triangles on spherical surfaces, guide them towards non-Euclidian geometry. Experienced educators like Gary are probably very adept at this. However, I think the reality of the situation is that most math teachers are not.

From the perspective of this student, the “teaching methods” did not change as I got older. With one exception, my math teachers adhered rigidly to the following procedure:

1. lecture to blackboard for entire class period
2. assign dozens of homework problems
3. test on material
4. rinse and repeat

How many math classes have you taken that followed this pattern? How many did not? There is an urgent need for the kind of teacher training Gary describes, where the focus is on personalized student development. Too many teachers are caught up in teaching the content, when they should be facilitating student learning instead.

In conclusion:

Does the nature of mathematics change as students get older or is it only the teaching methods that change?

Yes, a student’s model of the “nature of math” can change as that student grows older and discovers new results from the field of mathematics. I also think it’s arguable that the “nature of math” is not necessarily static, as presumed above, but that Gödel’s Incompleteness Theorem fundamentally changed the “nature of math” by using mathematics as a tool for analyzing itself — giving birth to metamathematics.

No, teaching methods do not change as the student grows older, but they do vary from teacher to teacher. In general, I think the “typical math teachers” need to take a cue from Gödel and start thinking more outside the box. The mathematics classroom needs to shift from its lecture/homework/test/repeat cycle, where math is essentially taught using an “argument from authority“, to an experimental environment where students are encouraged to question the information they receive.

Today’s #mathchat was a repeat of last Thursday’s discussion on “Mathphobia”. One of my questions in Thursday’s chat prompted a very insightful commentary from Gary Davis, a.k.a. @RepublicOfMath. With this new evidence in mind, I tried to observe today’s #mathchat with a fresh perspective. I couldn’t quite condense my thoughts into 140 characters, so I’m taking this opportunity to summarize what I learned from the experience.

First, I think its important to clarify what is meant by “mathphobia”. For the sake of clarity, I’ll use the term “mathphobia” in the same sense as @RepublicOfMath‘s article. Mathphobia is a condition where an individual is terrified of mathematics to the point of feeling physically sick at the thought of math. I’ll use the term “math anxiety” to refer to a lesser version of this condition, where an individual experience a fear of math that interferes with mathematical performance but is not as completely disabling as mathphobia. In general, moderate symptoms of math anxiety are highly prevalent in society. As @ColinTGraham noted, research studies have shown that simply telling adults that they’re going to take a math test will cause their blood pressure to rise! I realize that this distinction between “math anxiety” and “mathphobia” is somewhat fuzzy, but for the sake of argument these labels will suffice for now.

Reviewing Thursday’s #mathchat archive, I think you can see two different conversation lines taking place. One conversation about mathphobia and another about math anxiety.

With regards to @RepublicOfMath‘s proposal that mathphobia is the result of abusive teachers, this makes a lot of sense from the standpoint of classical conditioning. If a student repeatedly has painful experiences with mathematics instruction, then the student will gradually learn to associate the two. As a consequence, experiencing any subsequent mathematical instruction will automatically trigger a painful response.

With math anxiety, there are similar mechanisms at work. For example, the rise in blood pressure in preparation for a math test can be interpreted as a conditioned response to the need for an increase in cognitive processing. The high prevalence of math anxiety symptoms suggests that math anxiety can develop with or without “abusive teachers”. I think that a variety of the “mathphobia causes” discussed in Thursday’s #mathchat may contribute to math anxiety in some form or another, but may not be a cause of the more extreme mathphobia as described above.

With today’s #mathchat, I saw something a little bit different happen. The conversation took a turn towards “math avoidance” – the lack of participation in mathematical activities. Here I think we see the crux of the problem. When a student develops math anxiety or mathphobia, that student begins a behavioral pattern of math avoidance. This behavior is self-reinforcing because it allows the student to avoid the painful stimuli associated with math. In order to undo the association that underlies the math anxiety or mathphobia the student needs to be presented with stimulus-response situations that are positive, but when the student avoids math altogether this becomes a difficult task.

The other complication that math avoidance presents is that it becomes difficult to distinguish between students who suffer from math anxiety or mathphobia, and those who are avoiding it for other reasons. Those reasons might be a lack of perceived relevance, a negative social image of math, or a lack of self-confidence. Many of these issues were identified in Thursday’s #mathchat, but the focus of today’s chat really tied them all together for me.

In conclusion, I think we need to address math anxiety and mathphobia from two directions. First, the classroom needs to be a safe environment where students are free to make mistakes and learn from them rather than being punished for them. Secondly, the behavior of math avoidance needs to be addressed. In order to facilitate the extinction of the conditioned stimulus-response to math, students need to be exposed to math in a positive environment. At first glance, it may seem like this is “treating the symptom rather than the cause”. However, if teachers do not provide temporary relief for the symptom of math avoidance, it won’t be possible to “treat the cause” of math anxiety or mathphobia.

Some questions for further discussion:

• Where does one draw the line between “math anxiety” and “mathphobia”?
• How can educators address “math avoidance” behaviors?
• What are the best practices for creating and maintaining an empathetic and non-threatening mathematics classroom?

It’s been awhile since I blogged, so I thought I’d take a moment to talk about couple interesting math problems that came up in a conversation I, @SuburbanLion, had on Twitter with @MathGuide, @RepublicOfMath, and @GMichaelGuy about a month ago. The topic of discussion was the role of rationalization problems in Algebra II and whether or not the current curriculum addresses the “conceptual core” of these problems.

A common example that one would see in an Algebra II course is:

• Rationalize the denominator of $$\frac{1}{\sqrt{2}}$$

Or simply:

• Rationalize $$\frac{1}{\sqrt{2}}$$

The expected answer for this problem can be obtained by multiplying the numerator and denominator both by $$\sqrt{2}$$ to get: $$\frac{\sqrt{2}}{2}$$. Students might be assigned dozens of such problems in Algebra II. The question to be asking is “Why?”.

I suspect that the obvious answer is historical tradition. These math problems have been passed down from generation to generation as “standard Algebra II problems”, and even the new Core Standards includes “rewrite expressions using radicals and rational exponents” as an objective. Instead of treating these problems as a “means to an end”, these problems have become something of an end in themselves. Algebra II students learn to rationalize expressions because that’s what they’re going to be tested on. End of story.

The real reason for having these problems in Algebra II goes deeper than that. The Core Standards hits on this reason (at least partially) with one of the additional objectives: “Understand that rational expressions form a system analogous to the rational numbers, closed under addition, subtraction, and division by a nonzero rational expression.” While this objective is not specifically talking about radical expressions, the core concept is the same. More concisely, we might say that the important point of rationalizing radical expressions is to come to the conclusion that $$\mathbb{Q}+\mathbb{Q}\sqrt{p}$$ is a field.

Ironically, the 93 page Core Standards does not even mention the word “field” even though this is essentially the core concept that students are learning about. Students shouldn’t be rationalizing expressions just for the sake of rationalizing expressions, they should be exploring the intermediate steps between the field of rational numbers and the field of algebraic numbers. By the way, the phrase “algebraic number” doesn’t appear in the Core Standards either!

To make things interesting, G. Michael Guy presented a couple rationalization problems that are typically not included in Algebra II problem sets. These are actually really great examples of the potential complexity involved in rationalization problems.

Let’s warm up with the first one, which is significantly easier:

• Rationalize $$\frac{1}{1+\sqrt[3]{2}}$$

This one has an elegantly simple solution using the sum of cubes factorization:

• $$a^{3}+b^{3} = (a + b) \cdot (a^{2}-ab + {b^{2}})$$

Making the substitutions a = 1, b = $$\sqrt[3]{2}$$, we can take advantage of this product to rationalize the denominator:

• $$\frac{1}{1+\sqrt[3]{2}}\cdot\frac{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}}{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}} = \frac{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}}{1+\sqrt[3]{2}^{3}} = \frac{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}}{3}$$

This solution is simple enough that this could almost pass for an Algebra II problem. Rationalization problems in Algebra II are something of a gimmick: the problems chosen are special cases designed to have an easy answer. The methods taught in the textbook will solve the given problems, but they don’t generalize well to the larger class of problems. The techniques used in Algebra II provide very little help in rationalizing an expression like $$\frac{1}{1+\sqrt[3]{5}+\sqrt[3]{3}^{2}+\sqrt[3]{2}}$$!

Before we attempt something like this, lets go back to $$\frac{1}{1+\sqrt[3]{2}}$$ and come up with a method that will generalize well. This is where easy problems come in handy as a test bed for discovering the broader patterns. The general case of rationalizing $$\frac{1}{x_{0}+x_{1}\sqrt[3]{2}+x_{2}\sqrt[3]{2}^{2}}$$ can be reasonably done by hand.

The method used here is not likely to be seen in a typical Algebra II classroom, as it relies on concepts from Linear Algebra which typically aren’t addressed until later. Seems a little backwards if you ask me. The trick here is to think of the product $$(x_{0}+x_{1}\sqrt[3]{2}+x_{2}\sqrt[3]{2}^{2})(y_{0}+y_{1}\sqrt[3]{2}+y_{2}\sqrt[3]{2}^{2})$$ as the product of a matrix and a vector:

• $$M_{x}\cdot\overrightarrow{y} = [1, 0, 0]$$

Solving this equation is then simply a matter of multiplying both sides by $$M_{x}^{-1}$$. This method extends nicely to even harder problems, including $$\frac{1}{1+\sqrt[3]{5}+\sqrt[3]{3}^{2}+\sqrt[3]{2}}$$. Inverting a 27 by 27 matrix is not something I’d want to be doing by hand, so this is where computers come in handy. Here’s an algorithm for rationalizing $$\frac{1}{1+\sqrt[3]{5}+\sqrt[3]{3}^{2}+\sqrt[3]{2}}$$ in Sage. Compare this with Wolfram|Alpha’s result.

I’m a strong believer that computing should play a larger role in mathematics education than it is presently. Not only should the curriculum be addressing the fact that the algebraic numbers form a field, but also that all algebraic numbers are computable numbers. By shifting the focus of discussion from solving problems to finding an algorithm for solving those problems, we can reveal a better picture of the mathematics behind the problem. Simple problems worked out by hand play an important role in the process of designing an algorithm, but an ability to generalize the solution should be the larger goal. If the rationalization problems that students are completing by the dozens do not lead the student in the direction of a general solution, then those problems are not doing their job. Perhaps some “harder” problems are necessary to encourage that generalization.

For the record, “computable numbers” are not referenced once in the Core Standards. It’s hard to give students a 21st century education when the math curriculum is trapped in the early 1900s.

What follows below is the feedback I provided on the proposed Core Standards for Mathematics.  These represent my own opinions on the direction mathematics reform should take.  As far as I know, the changes I propose have not been sufficiently supported by research.  However, I hope I may provide a fresh perspective on the direction the mathematics curriculum should take to address some of the existing problems.

I’d like to start with some background about myself, to provide a context for this critique. I was an accelerated math student in high school and majored in Mathematics in college. These views are my subjective interpretations of the mathematics curriculum as I experienced it, and the areas of mathematics in college that I felt unprepared for. My objection to the proposed Core Standards is that I do not view them as reforming these areas where I felt unprepared. Instead, all the Core Standards seem to do is set in stone the same failing curriculum I experienced as a student.

Overall I feel that the Standards for Practice expressed on pages 4-5 are solid goals for mathematics education to strive for. However, my major critique of the Core Standards is that I do not think they are sufficient to meet these goals. Two of the Standards for Practice strike me as being unsupported by the proposed curriculum: (3) Construct viable arguments and critique the reasoning of others and (5) Use appropriate tools strategically. The former requires a solid foundation in logic, set theory and critical thinking, while the latter requires an introduction to computation science. The standards that follow do little to reinforce these skills.

In order for students to construct and critique arguments, the students must first know the basic structure of an logical argument. How can students be expected to give valid arguments when the definitions of validity, soundness, completeness, and consistency are omitted from the mathematics standards? The only objective that seemed to actually address this was in the High School Algebra Standards: “Understand that to solve an equation algebraically, one makes logical deductions from the equality asserted by the equation”. I respect that this objective is included, but don’t think that the curriculum leading up to it adequately supports it. When I was first exposed to college level mathematics, the notation system of formal logic was used extensively by my professors. My education leading up to that point had not covered this notation, and it felt like I was learning a second language in addition to the mathematical concepts. The notions of formal logic are not complicated, but earlier exposure to these ideas would have made me more prepared for college mathematics.

In my opinion, the K-8 standards are too focused on number and computation. The objectives covered in the K-8 curriculum reflect a notion of numbers consistent with the view of mathematics in the early 1800s. In 1889, when Peano’s Axioms were introduced, the mathematical notion of a “natural number” changed. The “natural numbers” have been redefined in terms of set theory since the 1900s. Students need to have a concept of numbers that are consistent with the modern set theoretic constructions. The pen-and-paper computations covered in elementary school are valuable, but have in many instances been replaced by technology. It’s not enough for students to know how to perform addition, but the modern student needs to also know that the operation of addition is analogous with joining sets. In mathematics, number theory is built upon the foundation of set theory. Focusing on numbers before sets is illogical considering the hierarchy of mathematical knowledge.

Set theory is also based on logic, which is also missing in action. Several of the objectives mention making logical conclusions about problems, but where’s the logic? The mathematical definitions of “and”, “or”, “xor”, “not”, “nor”, “nand”, “implies”, “for every”, “there exists” and “proves” are absent from the standards. The relationship between the basic operations of logic and those of arithmetic needs to be thoroughly established. This is not only important from a mathematical standpoint, but it is essential to learning how computational technology works. The operations of arithmetic can be build from the basic building blocks of logic, and that is how computers manage to produce the calculations that they do. All students will work with technology in some manner or another, and developing an understanding of how that technology works will make them more effective users of technology.

The focus of the K-8 curriculum is to develop students’ understanding formal axiomatic systems. Mathematics should be presented in the form a game. The rules of the game determine patterns that are produced in the process. Too much of a focus on the outcomes underemphasizes the importance of the rules to begin with. Algebra, in particular, requires students to rewrite expressions using the properties of numbers. The failure of the curriculum is that students have no prior experience with substitution systems. The algebra student is essentially thrown into the game without knowing the rules. It’s no wonder that algebra presents such a challenge for mathematics eduction.

In the High School Standards, my main objection is to the separation between the general curriculum and the STEM curriculum. Most of the objectives labeled as STEM objectives, should be included in the general curriculum. STEM students need a more thorough picture of mathematics than that presented here. As an example, complex numbers are treated as a STEM only topic in the standards. The Fundamental Theorem of Algebra depends on the field of complex numbers and all students should be exposed to this result. Students preparing for STEM need to go beyond complex numbers to constructions such as dual numbers and quaternions which would help prepare students to acquire a more general notion of Clifford algebras in college. These tools may seem obscure to traditional educators, but are essential tools to physicists and engineers. Quaternions have several useful properties that make them ideal for modeling rotations, and dual quaternions can be used to represent rigid transformations.

One of my pet peeves about high school mathematics is that the picture of physics presented there was radically different than the picture presented in college. As an example, consider the following algebra problem: “Joe and Sue live 10 miles apart. Joe heads towards Sue’s house at 5mph and Sue heads towards Joe’s house at 3mph. If they both leave at the same time, how long until they meet?” Questions like this are usually represented as linear equations, like “3x+5x=10”. However, this gives students the false impression that this is an accurate model of velocity in the real world. The fact of the matter is that this equation is only reasonable for small numbers. A change in the numbers included in this problem could invalidate the model. Consider the modified question, “Joe and Sue live 10 light-years apart. Joe heads towards Sue’s house at .8c and Sue heads towards Joe’s house at .9c. If they both leave at the same time, how long until they meet?” Under these figures, a linear model of time is no longer accurate. Time slows for Joe and Sue relative to a stationary observer, and the question of “how long until they meet” is more complicated than it appears on the surface. If they each start a stopwatch at the moment of departure, their clocks will have different readings when they meet. Students in a STEM course of study need to understand that velocity in space-time is fixed at the speed of light, and what we perceive as motion is a rotation of this space-time vector.

There are several other topics that I consider important for STEM students that go beyond the standards. The study of triangles in geometry needs to extend to ordered triangles, and the linear algebra needed to manipulate such triangles. The notion of “angle” as presented in the high school curriculum is insufficient. Students need to start thinking about angles as they relate to the dot product (inner product) of vectors. The trigonometric functions of sine and cosine need to be connected to complex exponents by way of Euler’s formula: “e^ix = cos x+i sin x”. The properties of logarithms also need to be explicitly covered in the curriculum. Covering these notions in the high school curriculum would make students better prepared for subsequent studies of calculus and geometry.

Some of these suggestions may seem like obscure areas of mathematics, but my argument is that they shouldn’t be. If the purpose of K-8 is to develop an understanding of what formal axiomatic systems are, then the focus of 9-12 should be on discovering the useful properties that result from the standardly accepted axioms. I once conducted a job interview where a mathematics student, like me, was applying for a software engineering position, also like me. My employer had brought me into the interview to determine whether or not the candidate was ready to apply his mathematically expertise to computer programming. During the interview, the candidate mentioned quaternions as one of his areas of interest. In the software developed at this company, orientations and rotations are routinely stored and manipulated as quaternions. When I asked how the candidate would use quaternions to compute a rotation, he was stumped. He also became extremely interested in the interview at that point and was eager to learn more about the technique. My question had revealed that the abstract mathematics he was familiar with had a real purpose behind it – a practical use within the field of computer science. It’s this kind of disconnection between abstract and applied applied mathematics that seems to be one of the major problems with mathematics education.

Abstraction plays a large role in mathematics and it’s usually the use of mathematics in other disciplines which connects it to students’ real world experiences. I was fortunate enough to have learned most of my mathematical knowledge in the context of computer science. Mathematics and computer science share a good deal of common ground. Furthermore, working with computers has become an essential skill for career-readiness in modern times. Learning how technology works adds to ones ability to effectively use that technology. When the Standards for Practice call for students to use computational tools proficiently, the lack of standards addressing how that technology works will hinder the obtainment of that goal. When students use computers or calculators to produce computations, they need to know that they are not working with “real numbers”. Not all real numbers are computable. Until the mathematics curriculum prepares students to tackle such notions, students will not be college or career ready.

One of the considerations for the Core Standards is that they address 21st century skills. Reading the mathematics standards, I do not think that this consideration has been met. The mathematics included in this curriculum is dated and fails to address the advances made in the past century. The Core Standards for math focus on applying known algorithms to problems with known solutions. A 21st century education needs to focus on creating and analyzing algorithms. Students not only need to know algorithms for solving mathematics problems, but need to be able to think critically about the efficiency of those algorithms. The Core Standards are a step in the wrong direction in this regard. All these standards will accomplish is that mathematics education will be catered to address the specific problems covered by the standards. Teachers will teach to the test and the critical thinking skills hinted at in the Standards for Practice will be lost in the assessment process.

I appreciate that these standards are chosen based on evidence from educational research. However, I think that the research supporting these standards is biased by the currently existing assessments. The evidence showing that American students are behind in math means there is still a gap between the standards in place and the skills students need to be college and career ready. A fixed set of national standards is not a viable solution to the problem. What the education system needs is a solid framework for an experimentation cycle in which standards are continually tested and revised to meet the changing needs of students.