Category: Math

Posted on
by

Hello! My name’s Ryan and I’m an “undecided” voter.

No, it’s not what you think.

I’m not undecided between these guys:

Obama Romney

There’s no way in hell I’m voting for Romney.

I’m not an idiot as Bill Maher not-so-subtly suggested last week. (It’s okay Bill, I can take a joke)

I’m undecided between these guys (and gal):

Obama Johnson Stein

Mathematician and author John Allen Paulos described the situation a little more elegantly:

I’d like to believe that I fall into the “unusually thoughtful” category and wanted to share my perspective.

FULL DISCLOSURE: This is my personal blog and obviously biased by my opinions. I’m a member of the Green Party and have made a “small value” donation to the Stein campaign. Despite my party membership, I try to vote based on the issues and not the party. I voted for Obama in 2008 and voted for Ron Paul in the 2012 GOP primary. While I’m not technically an “independent” due to my affiliation with the Greens, I’m probably about as close to one as it gets.

Let’s start with a little historical background and work our way forward from there.

The Nader Effect

My first voting experience was in the 2000 election. I didn’t like either Gore or Bush, and ended up gravitating towards the Nader campaign. His positions on the issues most closely aligned with my own, so I did what seemed like the most rational thing to do at the time. I voted for him.

After the election, Nader (and the Green Party in general) received a large amount of criticism from Democrats for “spoiling” the election. The Democrats argued that votes cast for Nader in key states like Florida, would have been otherwise been cast for Gore. The counter argument is that Bush v. Gore was decided by the Supreme Court, but I won’t get into that.

From my perspective, my vote for Nader in this election could not be counted as a “spoiler”. I was living in California at the time, and the odds of California’s votes in the Electoral College going to Bush in the 2000 were negligible. My vote for Nader was completely “safe” and allowed me to voice my opinion about the issues I cared about. However, this notion of a “spoiler vote” forever changed how I thought about my voting strategy.

Independence of Irrelevant Alternatives

In the 1950s, economist Kenneth Arrow conducted a mathematical analysis of several voting systems. The result, now known as Arrow’s Impossibility Theorem, proved that there was not ranked voting system that could satisfy the following conditions for a “fair” election system:

  1. It accounts for the preferences of multiple voters, rather than a single individual
  2. It accounts for all preferences among all voters
  3. Adding additional choices should not affect the outcome
  4. An individual should never hurt the chances of an outcome by rating it higher
  5. Every possible societal preference should be achievable by some combination of individual votes
  6. If every individual prefers a certain option, the overall result should reflect this

Arrow was largely concerned with ranked voting systems, such as Instant Run-off Voting, and proved that no such ranking system could ever satisfy all of these conditions. There are non-ranked voting systems that meet most of these conditions, such as score voting, but one of these conditions of interest that our present system doesn’t meet is number 3. This condition goes by the technical name of Independence of irrelevant alternatives. The idea is that the outcome of a vote should not be affected by the inclusion of additional candidates. In other words, there should never be a “spoiler effect”.

What I find interesting here is that the very mechanics of our voting system lead to a situation where the outcome of elections is controlled by a two party system. It forces citizen to vote tactically for the “lesser of two evils”, while from my perspective both of those “evils” have gotten progressively worse. George Washington warned of this outcome in his farewell address:

However [political parties] may now and then answer popular ends, they are likely in the course of time and things, to become potent engines, by which cunning, ambitious, and unprincipled men will be enabled to subvert the power of the people and to usurp for themselves the reins of government, destroying afterwards the very engines which have lifted them to unjust dominion.

Until we can address the issues inherent in our voting system itself, I’m left with no choice but to vote strategically in the election. My policy for voting is a tactic of minimaxing: minimizing the potential harm while maximizing the potential gain. It’s with this strategy in mind that I turn to the options of the 2012 presidential race.

Quantifying Politics

In order to apply a mathematical analysis to voting, it is first necessary to have some way of quantifying political preferences. As a method of during so, I’ll turn to the so called Nolan Chart. An easy way to find out where you stand on the Nolan Chart is the World’s Smallest Political Quiz. Here’s where it places me:

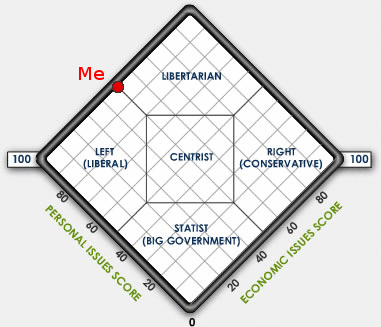
Here’s where I’d place the 2012 candidates:

Note that this is my subjective opinion and may not necessarily reflect the opinions of the candidates themselves. It’s also important to note that this is a simplified model of political disposition. There are other models, such as the Vosem (восемь) Chart that include more than two axes. If you were, for example, include “ecology” as a third axis, this would place me closer to Stein than Obama and closer to Obama than Johnson. The resulting distances to each are going to vary depending on what axes you choose, so I’m just going to stick with the more familiar Nolan Chart.

Since I’m politically equidistant from each of the candidates, my minimax voting strategy would suggest that I vote for the candidate that has the highest chance of winning: Obama. However, there are many more variables to consider that might result in a different outcome. One of those variables is something I call “political flux”.

Political Flux

People change. It’s a well known fact of life. Changes in political opinions are no exception. If you look at the stances that Obama and Romney have made during this campaign, and compare those to their previous positions, I think you’ll see a trend that looks something like this:

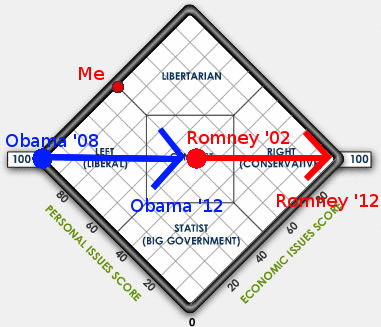
Obama campaigned hard left in 2008, but during his term in office his policies have shifted more towards the center. Romney campaigned in the center while he was running for governor of Massachusetts, but has shifted more towards the right during his presidential campaign. These changes are highly concerning to me, because both candidates are shifting away from my position. Thus, while Obama is closer to me on the political spectrum, the fact that he is moving away from my position makes the long term pay-offs lower than they would be if he had “stuck to his guns”. In turn, this makes the 3rd party candidates a more appealing option.

I might even go so far as to suggest that this “political flux” is the reason why these 3rd party candidates are running. Statistically, their odds of winning are too low to change the outcome of the election. However, they can influence the direction of the political discourse. The more people that vote for those candidates, the more likely that future candidates venture in those respective directions. This vote comes at a “risk” though, as those 3rd party candidates run the risk of “spoiling” the election for a less undesirable candidate. The level of this this risk varies from state to state due to the electoral college system.

The Electoral College

A popular vote is not enough to win the election. The president is selected by an Electoral College that gets a number of votes based on a (mostly) population proportional system. For some of these states, the polls predict a pretty solid winner and loser for the presidential race. For others, the state has a tendency to lean right or left. According to The New York Times, the following states are considered a “toss-up” in the upcoming election:

  • Colorado
  • Florida
  • Iowa
  • North Carolina
  • New Hampshire
  • Nevada
  • Ohio
  • Virginia
  • Wisconsin

If you are living in one of these states, the risks of voting for a third party are greater because your vote will have a higher chance of “spoiling” the election for one of the candidates. I happen to live in Virginia — one of the 2012 “battleground” states. I foresee a large number of attack ads in my near future. The big question is, is the pay-off worth the risk?

Aikido Interlude

For the past couple months, I’ve been studying Aikido — a martial art that might be best described as “the way of combining forces”. The idea is to blend ones movements with those of the attacker to redirect the motion of the combined system in a way that neither individual is harmed by the result. As a lowly gokyu, I still have a lot to learn about this art, but I find some of the core principals behind it rather insightful from a physical and mathematical perspective.

The basic idea is a matter of physics. If an object has a significant amount of momentum, then it takes an equal amount of momentum to stop it. However, if you apply a force that is orthogonal (perpendicular) to the direction of motion, then its relatively easy to change the direction of motion. You don’t block the attack in aikido. You redirect the attack in a way that’s advantageous to your situation. You can see the basic idea in my crude drawing below:

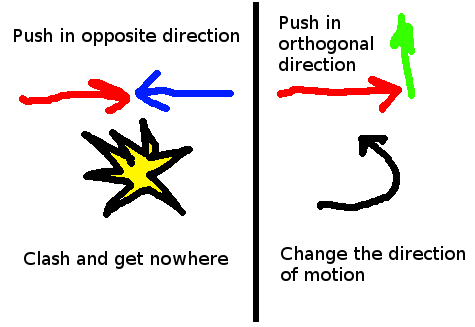
The result of this is that many aikido techniques end up having a “circular” sort of appearance. In reality, it’s the combination of the attacker’s momentum and the orthogonal force applied by the defender that cause this. See if you can spot this in the following video of Yamada sensei:

So what does this have to do with voting?

Well consider my position on the Nolan Chart and the direction that the two major candidates are moving in. As much as I would like to shift the debate to the left, it would require a significant amount of political force and time to negate this momentum towards the right and even longer to push it in the opposite direction. It would be much more efficient to push “north” and allow the momentum to carry the political culture towards my general position.

In other words, voting for Gary Johnson might actually be the path of least resistance to my desired policies.

Metagaming the Election

Here you can start to see my predicament. Part of me wants to vote for Gary Johnson, because I think that doing so would be mostly likely to shift the debate in the direction I want it to go. Part of me wants to vote for Jill Stein, as doing so would help strengthen the political party that I belong to. Part of me wants to vote for Barack Obama, but only because doing so would have the greatest chance of preventing a Romney presidency. According to the latest polling data, the odds of Obama being re-elected are 4:1. Those are pretty good odds, but this is a high stakes game. It sure would be nice if there was a way to “have my cake and eat it too”.

It turns out that there is.

I can metagame the election.

The idea of metagaming, is that it’s possible to apply knowledge from “outside the game” to alter one’s strategy in a way that increases the chance of success. In this case, I’ve decided to employ a strategy of vote pairing.

You see, I live in the same state as my in-laws who traditionally vote Republican. However, despite a history of voting GOP, they’re both very rational people. Romney keeps shooting himself in the foot by saying things that are downright stupid. Screen windows are airplanes? Free health care at the emergency room? The more Romney talks, the easier it becomes to convince rational people that he’s unfit to be president.

After many nights of debate, we’ve come to the realization that we’re only voting for one of the two major parties because the other party is “worse”. From there, a solution presents itself: “I’ll agree to not vote for Barack Obama if you agree to not vote for Mitt Romney”. This agreement is mutually beneficial to both parties involved. Without this agreement, our votes just cancel each other out. With the agreement, the net benefit to each candidate is still zero but now those votes are free to be spent elsewhere. The end result is that we each have a larger impact on the presidential election without altering the outcome.

With the vote pairing secured, I’m free to vote for Stein or Johnson at my own discretion. Both of these candidates agree on what I think is the most important issue: ending our “wars” (of which there are too many to list). They differ on a number of issues, particularly on economics and the environment. Personally, I think that the Greens and Libertarians need to meet half-way on the issues for an Eco-libertarian ticket. Jill Stein needs to recognize that the US Tax Code is a mess and needs reform. Doing so can help eliminate corporate handouts, many of which go to industries that adversely affect public health. Gary Johnson needs to recognize that laissez-faire economic policies alone will not fix our broken health care system or halt the impending climate change. I’m going to be looking forward to seeing debates between Stein and Johnson which I think will highlight the complexities of these issues and hopefully identify some possible solutions.

That’s great, but what can I do?

You can enter a vote pairing agreement with someone of the opposite party. If you would ordinarily vote for the Democrats, you can click here to find out which of your Facebook friends “like” Mitt Romney. If you would ordinarily vote for the Republicans, you can click here to find out which of your Facebook friends “like” Barack Obama. Talk about the issues that are important to you in the race, discuss your objections to the other candidate, and if things go well, agree to both vote for a third party. If everyone did this, one of those 3rd parties might actually win. Even if it doesn’t change the outcome, you’ll know that your vote didn’t “spoil” the election for your second choice.

If you want to go one step further, you can Occupy the CPD. Sign the petition to tell the Commission on Presidential Debates that you think we should hear from all qualified candidates and not just the two that they think we should hear from.

Finally, research the alternative parties and join one that matches your personal beliefs. Even you end up voting for one of the two major parties, joining a 3rd party and supporting that movement can have a significant effect on future campaigns. Here’s a few links to get you started:

Posted on
by

This weekend marks the 3rd Beta World Event for Guild Wars 2. I wrote a little bit about my general experiences in the first BWE, but this time I’m focusing on a very specific area of the game. In the first BWE, I was just playing the game and having fun with it. In the second BWE, I started to do a lot more “testing”. In particular, one of the things I was testing was the “Sharper Images” trait.

Sharper Images (SI) is a Dueling trait that causes critical hits from Illusions to inflict bleeding for 5 seconds. This trait was bugged in the first BW1 and didn’t work at all. In the second BWE1, it worked as described but a second phantasm trait called “Phantasmal Haste” was bugged resulting in some crazy damage output. This means that I didn’t get a very good perspective on how these two traits would work together, but that’s okay because I can do the math! In addition to seeing how the phantasm related traits would interact together, I also wanted to find out which stats to gear for in order to maximize my damage. In order to do this, we first need some information about how damage is calculated in GW2. Assuming a level 80 character:

  • Pandara_RA! at Team Legacy worked out the following formula for the base damage of an attack: $$ Base Damage = \frac{(Power) \cdot (Weapon Damage) \cdot (Skill Coefficient)}{Target Armor} $$
  • The chance of getting a critical attack is determined by the Precision above the base: $$ CritRate= \frac{4 + (Precision – Base)/21}{100} $$
  • When an attack criticals, it hits for 50% more damage plus any bonus to critical damage (Prowess). With this, we can find out the average damage of an attack using: $$ Direct Damage = (Base Damage) \cdot (1+(Crit Rate) \cdot (0.5+\frac{Prowess}{100})) $$
  • The last piece of information we need is the bleeding damage, which is dependent on condition damage (Malice). According to the GW2 wiki this is determined by $$ \frac{damage}{second} = 40+0.05 \cdot (Malice) $$. The bleed duration of 5 seconds can be improved through stats, but only pulses once per second. This means that we can round the duration down to find the number of pulses and find the total bleed damage: $$ \frac{damage}{second} \cdot \lfloor duration \rfloor $$

To get a rough estimate of Phantasm DPS, I put these formulas together with some various equipment set-ups and trait choices. You can download this spreadsheet here. To make things simplier, I focused entirely on “Illusionary Duelist” with SI because I knew it hits 8 times every 10 seconds. I also had to make several assumptions about how certain traits would stack, and all of this is subject to change when the game is released anyway. Despite these shortcomings, I found several interesting results:

  • Without any bonus condition damage, SI can add about 10%-20% damage depending on the target’s armor (best against higher armor foes) when used in conjunction with Phantasmal Fury. This puts it on par with most damage traits at the adept level.
  • With a skill coefficient of about 0.5 (a total guess BTW), the direct damage builds and condition damage builds I tried seem to even out in terms of potential damage. A lower skill coefficient tends to favor condition damage and a higher one favors direct damage.
  • Chaotic Transference bonus seems lack-luster relative to the heavy investment.
  • Phantasmal Strength and Empowered Illusions complement each other well in a power Build, but the investment for Phantasmal Strength doesn’t seem worth it in a condition damage build.
  • Phantasmal Haste tends to work better with a condition damage build than a power build. You don’t need to hit hard with SI, you just need to hit often.
  • Investing 20 points into Domination can have a big effect on condition damage builds because it extends bleeds for an extra tick. This makes Lyssa’s Runes a potentially interesting choice with SI because of the +10% condition duration, allowing you to spend 10 of those points from Domination elsewhere with minimal DPS loss.
  • The Rampager jewelry seems to be a better choice than Rabid for a condition damage build with SI. There’s no point to having strong bleeds if you aren’t applying them frequently enough.

There’s still a lot more analysis to be done here and some empirical data to collect in BWE3 to verify these findings, but the results look promising. As it stands, you can make SI work in either a direct damage phantasm build or condition damage build with the appropriate gear. Small tweaks to the skill coefficient can keep the two builds competitive if necessary. This fits with Arena.Net’s philosophy of having multiple play-styles be equally viable.

I’d encourage you to try out the spreadsheet with other gear and build combinations that I didn’t try. If you’re feeling adventurous, you might even extend it to include skills other than iDuelist or other traits I may have overlooked. If you find out any more information about how phantasm damage is calculated I’d love to hear about it in the comments!

Happy theory-crafting!

Update: BWE3

I did a little testing during BWE3, regarding the attack rates and skill coefficients of the different phantasms. This information should help give an idea of how much each phantasm benefits from stacking Power vs stacking crit/condition damage for Sharper Images. Please note that my recharge times were approximated, and Sanek over at GW2Guru came up with somewhat different numbers. I’m including both my attack rates and his for comparison:

illusion Hits Recharge Attack Rate (hits/sec) Sanek’s Recharge Sanek’s Rate (Hit/sec) Approx. Skill Coef. DPS Coef. (Mine) DPS Coef. (Sanek)
iDuelist 8 10 0.8 7.5 1.066666667 0.228956229 0.183164983 0.244219978
iSwordsman 1 3 0.333333333 5.5 0.181818182 0.734006734 0.244668911 0.13345577
iWarlock 1 5 0.2 6 0.166666667 0.080808081 0.016161616 0.013468013
iBerserker 1 5 0.2 6 0.166666667 0.281144781 0.056228956 0.046857464
iMage 1 5 0.2 6.7 0.149253731 0.397306397 0.079461279 0.059299462
iDefender 1 3 0.333333333 4.5 0.222222222 0.131313131 0.043771044 0.029180696
iDisenchanter 1 3 0.333333333 4.5 0.222222222 0.131313131 0.043771044 0.029180696
iWarden 12 10 1.2 14 0.857142857 0.033670034 0.04040404 0.028860029
swordClone 3 3 1
staffClone 1 1 1
scepterClone 2 3 0.666666667
gsClone 3 2 1.5

Knowing that the skill coefficient for iDuelist is only 0.23, stacking for condition damage seems to be the best method to maximize damage over time with Sharper Images given a high enough crit rate to apply it consistently. As a general rule of thumb, if your crit rate is less than 50% then you should be gearing for power and if your crit rate is greater than 50% then you should be gearing for condition damage.

A few other interesting things to note:

  • iSwordsman has one of the best skill coefficients of any phantasm. If you’re not using Sharper Images and have Power oriented spec, you may want to try out the off-hand sword.
  • iWarlock’s DPS is pretty pitiful without conditions. I’m not sure what the bonus per condition is, but I’d recommend having two staff clones up with iWarlock since they have a much faster attack rate. Edit: 10% bonus per condition
  • iWarden has quick attack rate and is has an AoE attack, but remember that this Phantasm is stationary. You’re very unlikely to get all 12 hits against a real player.
  • iBerserker has slow recharge AoE attack that moves down a line. It might be possible to hit an opponent twice with this if they’re running in the same direction, but I can’t be sure about it.
  • The Greatsword clones have the fastest attack rate of any illusion according to my tests. It seems kind of odd that the best clone for Sharper Images would be on a weapon with no innate condition damage.
  • iMage has a high skill coefficient but low attack rate. At first glance, this looks like it would be better for a power build than condition build, but you should remember that he also applies Confusion on attack.
  • iMage and iDisenchanter have bouncing attacks that hit three targets: 1 enemy and 2 allies. I couldn’t seem to get it to hit the same enemy twice, but this is something to check for on release.
  • Keep in mind that my original spreadsheet assumes that you leave your Phantasms out all the time. As of BWE3, this is no longer the optimal play-style. If you decide to go with a Power build, you’ll probably get the best burst damage by using Mind Wrack right after your phanstasm’s first attack cylce. Likewise, Cry of Frustration can now dish out some major hurt if you’re built for condition damage.

Posted on
by

In a previous blog post, I made the claim that much of the math curriculum is ordered based on historical precedent rather than conceptual dependencies. Some parts of the math curriculum we have in place is based on the order of discovery (not always, but mostly) and while other parts are taught out of pure habit: This is how I was taught, so this is how I’m going to teach. I don’t think this needs to be the case. In fact, I think that this is actually a detriment to students. If we want to produce a generation of mathematicians and scientists who are going to solve the difficult problems of today, then we need to address some of the recent advances in those fields to prepare them. Students should not have to “wait until college” to hear about “Topology” or “Quantum Mechanics”. We need to start developing the vocabulary for these subjects much earlier in the curriculum so that students are not intimidated by them in later years.

To this end, I’d like to propose 5 mathematical breakthroughs that are both relatively recent (compared to most of the K-12 curriculum) while also being accessible to elementary school students. Like any “Top 5”, this list is highly subjective and I’m sure other educators might have differing opinions on what topics are suitable for elementary school, but my goal here is just to stimulate discussion on “what we could be teaching” in place of the present day curriculum.

#1. Graph Theory (c. 1736)

The roots of Graph Theory go back to Leonard Euler’s Seven Bridges of Königsberg in 1736. The question was whether or not you could find a path that would take you over each of the bridges exactly once.

Bridges of Königsberg

Euler’s key observation here was that the exact shapes and path didn’t matter, but only how the different land masses were connected by the bridges. This problem could be simplified to a graph, where the land masses are the vertices and the bridges are the edges.

This a great example of the importance of abstraction in mathematics, and was the starting point for the field of Topology. The basic ideas and terminology of graph theory can be made easily accessible to younger students though construction sets like K’Nex or Tinkertoys. As students get older, these concepts can be connected to map coloring and students will be well on their way to some beautiful 20th century mathematics.

#2. Boolean Algebra (c. 1854)

The term “algebra” has developed a bad reputation in recent years. It is often referred to as a “gatekeeper” course, which determines which students go on to higher level mathematics courses and which ones do not. However, what we call “algebra” in middle/high school is actually just a subset of a much larger subject. “Algebra I” tends focuses on algebra as it appeared in al-Khwārizmī’s Compendious Book on Calculation by Completion and Balancing (circa 820AD). Consequently, algebra doesn’t show up in the math curriculum until students have learned how to add, subtract, multiply and divide. It doesn’t need to be this way.

In 1854, George Boole published An Investigation of the Laws of Thought, creating the branch of mathematics that bears his name. Rather than performing algebra on numbers, Boole used the values “TRUE” and “FALSE”, and the basic logical operators of “AND”, “OR”, and “NOT”. These concepts provided the foundation for circuit design and eventually lead to the development of computers. These ideas can even be demonstrated with a variety of construction toys.

The vocabulary of Boolean Algebra can and should be developed early in elementary school. Kindergartners should be able to understand basic logic operations in the context of statements like “grab a stuffed animal or a coloring book and crayons”. As students get older, they should practice representing these statements symbolically and eventually how to manipulate them according to a set of rules (axioms). If we develop the core ideas of algebra with Boolean values, than perhaps it won’t be as difficult when these ideas are extended to real numbers.

#3. Set Theory (c. 1874)

Set Theory has its origins in the work of Georg Cantor in the 1870s. In 1874, Cantor published a ground breaking work in which he proved that there is more than one type of infinity — the famous “diagonal proof“. At the heart of this proof was the idea of thinking of all real numbers as a set and trying to create a one-to-one correspondence with real numbers. This idea of mathematicians working with sets (as opposed to just “numbers”) developed momentum in the late 1800s and early 1900s. Through the work of a number of brilliant mathematicians and logicians (including Dedekind, Russell, Hilbert, Peano, Zermelo, and Fraenkel), Cantor’s Set Theory was refined and expanded into what we know call ZFC or Zermelo-Fraenkel Set Theory with the Axiom of Choice. ZFC was a critical development because it formalized mathematics into an axiomatic system. This has some suprising consequences such as Gödel’s Incompleteness Theorem.

Elementary students probably don’t need to adhere to the level of rigor that ZFC was striving for, but what is important is that they learn the language associated with it. This includes words and phrases like “union” (“or”), “intersection” (“and”), “for every”, “there exists”, “is a member of”, “complement” (“not”), and “cardinality” (“size” or “number”), which can be introduced informally at first then gradually formalized over the years. This should be a cooperative effort between Math and English teachers, developing student ability to understand logical statements about sets such as “All basset hounds are dogs. All dogs are mammals. Therefore, all basset hounds are mammals.” Relationships can be demonstrated using visual aids such as Venn diagrams. Games such as Set! can further reinforce these concepts.

#4. Computation Theory (c. 1936)

Computation Theory developed from the work of Alan Turing in the mid 1930s. The invention of what we now call the Turing Machine, was another key step in the development of the computer. Around the same time, Alzono Church was developing a system of function definitions called lambda calculus while Stephen Kleene and J.B Rosser developed a similar formal system of functions based on recursion. These efforts culminated in the Church-Turing Thesis which states that “everything algorithmically computable is computable by a Turing machine.” Computation Theory concerns itself with the study of what we can and cannot compute with an algorithm.

This idea of an algorithm, a series of steps to accomplish some task, can easily be adapted for elementary school instruction. Seymour Papert has been leading this field with technologies like LOGO, which aims to make computer programming accessible to children. Another creative way of approaching this is the daddy-bot. These algorithms don’t need be done in any specific programming language. There’s much to be learned from describing procedures in plain English. The important part is learning the core concepts of how computers work. In a society pervaded by computers, you can either choose to program or be programmed.

#5. Chaos Theory (c. 1977)

Last, but not least, is Chaos Theory — a field of mathematics that developed independently in several disciplines over the 1900s. The phrase “Chaos Theory” didn’t appear in the late 1970s, but a variety of phenomena displaying chaotic behavior were observed as early as the 1880s. The idea behind Chaos Theory is that certain dynamic systems are highly sensitive to initial conditions. Drop a shot of half-half into a cup of coffee and the resulting pattern is different every time. The mathematical definition is a little more technical than that, but the core idea is relatively accessible. Chaos has even found several notable references in pop culture.

The other core idea behind chaos theory is topological mixing. This could be easily demonstrated with some Play-Doh (or putty) of two or more colors. Start by combining them into a ball. Squash it flat then fold it over. Repeat it several times and observe the results.

The importance of Chaos Theory is that it demonstrates that even a completely deterministic procedure can produce results that appear random due to slight variations in the starting conditions. This can even be taken one step further by looking at procedures that generate seeming random behavior independently of the starting conditions. We live in an age where people need to work with massive amounts of data. The idea that a simple set of rules can produce extremely complex results provides us with tools for succinctly describing that data.

Conclusion

One of the trends in this list is that these results are easy to understand conceptually but difficult to prove formally. Modern mathematicians seem to have a tendency towards formalism, which is something of a “mixed blessing”. On one hand, it has provided mathematics with a firm standard of rigor that has withstood the test of time. On the other hand, the language makes some relatively simple concepts difficult to communicate to younger students. I think part of the reason for this is that the present curriculum doesn’t emphasize the rules of logic and set theory that provide the foundation for modern mathematics. In the past, mathematics was driven more by intuitionism, but the math curriculum doesn’t seem provide adequate opportunities for students to develop this either! It might be argued things like “new math” or “Singapore math” are helping to develop intuitionism, but we’re still not preparing students for the mathematical formalism that they’ll be forced to deal with in “Algebra I” and beyond. Logic and set theory seem like a natural way to develop this familiarity with axiomatic systems.

Observers might also note that all five of these proposed topics are related in some form or another to computer science. Computers have been a real game-changer in the field of mathematics. Proofs that were computationally impossible 500 years ago can be derived a in minutes with the assistance of computers. It’s also changed the role of humans in mathematics, from being the computer to solving problems using computers. We need to be preparing students for the jobs computers can’t do, and my hope is that modernizing the mathematics curriculum can help accomplish this.

Do you have anything to add to this list? Have you tried any of these topics with elementary students? I’d love to hear about your experiences in the comments below.

Posted on
by

Gary Davis (@republicofmath) wrote an article that caught my attention called What’s up with pre-calculus?. In it, he presents a number of different perspectives on why Pre-Calc classes have low success rates and do not adequately prepare students for Calculus.

My perspective on pre-calculus is probably far from the typical student, but often times the study of “fringe cases” like myself can provide useful information on a problem. The reason why my experience with Pre-Calc was so atypical, is because I didn’t take it. After taking Algebra I, I had started down a path towards game programming. By the end of the following year, where I had taken Geometry, this little hobby of mine hit a road block. I had come to the realization that in order to implement the kind of physics that I wanted in my game I would need to take Calculus. I petitioned my counselor to let me skip Algebra II and Pre-Calc to go straight into AP Calculus. They were skeptical at first, but eventually conceded to my determination and allowed me to follow the path I had chosen.

Skipping from Geometry to Calculus meant that there were a lot of things that I needed to learn that first month that many of my peers had already covered. I had never even heard the word “logarithm” before, had no idea what e was, and had only a cursory understanding of trigonometry. These were the topics I had missed by skipping Pre-Calc, and I was fully aware of that, so I “hit the books” and learned what I needed to know about them. By the end of that first month I had caught up to the rest of the class and by end of the semester I would be helping other students with those very same topics.

I think the most obvious difference between myself and the “typical Calculus student” was the level of motivation. Many of the students in Calculus were there because “it would look good on a college application”. I was there because I wanted to be there. A common problem throughout math education is the “When am I ever going to use this?” attitude. I already knew where I was going to use the math I was learning. I had an unfinished game at home that needed a physics system, and every new piece of information I learned in Calculus made me one step closer to that goal. If you had ever wondered why a 4th order Runge-Kutta method is better than Euler’s method, try writing a platformer.

The second difference was a little more subtle, but there were some conceptual differences in how I thought about exponential, logarithmic, and trigonometric functions. The constant “e” wasn’t just some magic number that the textbook pulled out of thin air, it was the the unique number with the property that $$ \frac{de^x}{dx} = e^x $$ and $$ \int e^x dx = e^x $$. When it came to sine and cosine, I would think of them like a circle while my other classmates would picture a right triangle. They would hear the word “tangent” and think “opposite over adjacent”, but I thought of it more like a derivative. Sure, I had to learn the same “pre-calc” material as they did, but the context of this material was radically different.

A couple years ago I suggested that Pre-Calc should be abolished. The trouble with Pre-Calculus (at least in the U.S.) is that the course needs to cover a very diverse array of questions which includes exponential, logarithmic and trigonometric functions. I would argue that these concepts are not essential to understanding the basic foundations of Calculus. The math curriculum introduces the concept of “slope” in Algebra I, which is essentially the “derivative” of a line. There’s no reason why we should be sheltering students from language of Calculus. The concepts of “rate of change” and “accumulation” can and should be connected with the words “derivative” and “integral”, long before students set foot in the course we presently call Calculus. As students become more comfortable with these concepts as they relate to lines, parabolas and polynomials, then gradually step up the level of complexity. When students start to encounter things like surfaces of revolution, then they’ll actually have a reason to learn trigonometry. Instead of trigonometry being the arbitrary set of identities and equations that it might appear to be in pre-calc, students might actually learn to appreciate it as a set of tools for solving problems.

I think this issue of Pre-Calc is really a symptom of a larger problem. The mathematics curriculum seems to be ordered historically rather than conceptually. I’ve heard Pre-Calc described as a bridge to Calculus. This makes sense when you consider the historical development of Calculus, but not when considering the best interest of students in today’s society. Leibniz and Newton didn’t have computers. Who needs bridges when you can fly?

Posted on
by

Is “rationality” a measurable quantity?

In a previous blog post, I discussed some common logical errors that often arise in political discourse. This led to a rather interesting discussion on Twitter about political behaviors and how to model them mathematically (special thanks to @mathguide and @nesa_k!). One of the questions that came up this this discussion was how to define “rational behavior” and whether or not this is a measurable quantity. What follows is my hypothesis on “rational behavior”: what it is and how to measure it.

Please keep in mind that this is just a hypothesis and I don’t quite have the resources to verify these claims experimentally. If anyone has evidence to support or dispute these claims, I would certainly be interested in hearing it!

Defining “rational behavior”

Before we can begin to measure “rationality”, we must first define what it means to be “rational”. Merriam-Webster defines “rational” as “relating to, based on, or agreeable to reason”. The Online Etymology Dictionary describes the roots of the word in the Latin rationalis, meaning “of or belonging to reason, reasonable”, and ratio, meaning “reckoning, calculation, reason”. It’s also worthwhile to mention that ratio and rational have a distinct mathematical definition referring to the quotient of two quantities. Wikipedia suggests that this usage was based on Latin translations of λόγος (logos) in Euclid’s Elements. This same Greek word lies at the root of “logic” in English.

Based on these definitions and etymology, I think its fair to define rational behavior as “behavior based on a process of logical reasoning rather than instinct or emotion”.

Even this definition is far from perfect. In the context of game theory, “rational behavior” often defined as the process of maximizing benefits while minimizing costs. Note that by this definition, even single celled organisms like amoeba would be considered to exhibit “rational behavior”. In my opinion, this minimax-ing is a by-product of evolution by natural selection rather than evidence of “reason” as implied by the typical usage of the word “rational”.

I should also clarify what I mean by “logical reasoning” in this definition. In trying to quantitatively measure rational behavior, I propose that it makes sense to use a system of fuzzy logic rather than Boolean logic. By using the Zadeh operators of “NOT”, “AND”, and “OR”, we can develop an quantitative measure of rationality on a scale of 0 to 1. In logic, we say that an arguement is considered sound if it’s valid and its premises are true. Since we’re using the fuzzy “AND” in this model, the rationality measure is the minimum truth value of the logical validity and base assumptions.

Using this definition, we can also define irrational behavior as “behavior based on an invalid logical argument or false premises”. I’d like to draw a distinction here by defining arational behavior as “instinctive behaviors without rational justification”, to cover the amoeba case described above. An amoeba doesn’t use logic to justify its actions, it just instinctively responds to the stimuli around it.

Rationalism and Language

There’s an implicit assumption in the definition of “rational behavior” that I’ve used here, and that is that this requires some capacity for language. First-order predicate logic is a language, so the idea that “rational behavior” is language dependent should come as no surprise. In fact, the same Greek word “logos” from which “rational” is derived was also used as a synonym for “word” or “speech”. The components of language are necessary for constructing a formal system, by providing a set of symbols and rules of grammar for constructing statements. Add a set of axioms (assumptions) and some rules for inference, and you’ll have all the components necessary to construct a logical system.

A Dynamic Axiomatic System Model of Rational Behavior

A this point we can start to develop an axiomatic system to describe rational behavior. Using the operators of fuzzy logic and the normal rules of first-order logic we can create an axiomatic system that loosely has the properties we would expect of “rational behavior”. It’s very unlikely that the human mind uses the exact rules of fuzzy logic, but it should be “close enough”. We also have to consider that the basic beliefs or assumptions of a typical person vary over time. Thus, it’s not enough to model rational behavior as an axiomatic system alone, we must consider how that system changes over time. In other words, this is a dynamic system.

As we go through life, we “try out” different sets of beliefs and construct hypotheses about how the world works. These form the “axioms” of our “axiomatic system”. Depending on whether or not these assumptions are consistent with our experiences, we may decide to keep those axioms or reject them. When this set of assumptions contains contradictions, the result is a feeling of discomfort called cognitive dissonance. This discomfort encourages the brain to reject one of the conflicting assumptions to reach a stable equilibrium again. The dynamic system resulting from this process is what I would characterize as rational behavior.

One particularly powerful type of axiom in this system is labeling. Once a person takes a word or label and uses it to describe him or herself, the result is the attribution of large number of personal characteristics at once. The more labels a person ascribes to, the more likely it is that a contradiction will result. Labeling also has powerful social effects associated with it as well. Ingroups and outgroups can carry with them substantial rewards or risks depending on the context.

Rather than rejecting faulty axioms when confronted with cognitive dissonance, some individuals develop alternative methods of reducing the discomfort. The general term for pattern of behavior is called cognitive bias. This behavior can take a variety of different forms, but the one that is most relevant to this discussion is the confirmation bias. One of the ways in which the human brain can reduce the effects of cognitive dissonance is by filtering out information that would result in a contradiction with the base assumptions. Another relevant bias to consider is the belief bias, or the tendency to evaluate the logical validity of an argument based on a pre-existing belief about the conclusion.

Whatever form it may take, cognitive bias should be taken as evidence of “irrational behavior”. Not all cognitive biases are of equal magnitude, and some arguments may rely more highly on these biases than others. The goal here is not a Boolean “true” or “false” categorization of “rational” and “irrational”, but more of a scale like the one used by PolitiFact: True, Mostly True, Half-True, Mostly False, False, Pants on Fire. The method of applying truth values in fuzzy logic makes it highly appropriate for this purpose.

Examples in Politics

Consider this clip from The Daily Show. Using this clip may seem a little biased, but it’s important to remember that John Stewart is a comedian. Comedians have an uncanny knack for walking the fine line between “rational” and “irrational”, providing an interesting perspective to work with.

In the first example, we have the issue of Rick Santorum and JFK. After reading JFK’s speech on religious freedom, Santorum says that it made him want to throw up. In order to defend this statement, Santorum uses a good ole fashioned straw man argument by claiming that JFK was saying “no faith is not allowed in the public public square” when in fact JFK was saying “all faiths are allowed”. I think Santorum’s behavior here is a prime example of irrational behavior. Taking this position may very well earn him some votes with the deeply religious, but it’s clear that Santorum has some problems finding consistency between his personal beliefs and the First Amendment. His position is not based on a valid logical argument, but on a physical response to the cognitive dissonance resulting from his conflicting beliefs. This example also shows the power of deeply held self-labeling behaviors like religion.

Mitt Romney made some headlines with his “NASCAR Team Owner” blunder. It would appear that Mitt Romney had gone to Daytona to try and score some points with “average Americans”, but a slip of the tongue showed how out of touch he really is. To Romney’s credit, his behavior here is about half-rational. His assumptions are probably something like this:

  • I want people to vote for me.
  • People vote for someone they can relate to.
  • Most people know someone who likes NASCAR.
  • I know someone who likes NASCAR.

It makes sense from a logical standpoint, but it turns out that the person who Romney knows that likes NASCAR just happens to be a
“team owner” instead of a “fan”. This small detail makes it unlikely that people will relate to him, but at least the foundation of a logical argument is there.

This brings us back to Rick Santorum again. This time, Santorum calls President Obama a “snob” for “[wanting] every American to go to college”. Not only is this comment blatantly false, but he’s employing an ad hominem attack in lieu of a logical argument. This example draws a nice dichotomy between President Obama and Rick Santorum. The President is making a rational argument in favor of higher education which is well supported by evidence. By opposing this rational argument on a faulty premise, Santorum comes out of this situation looking mostly irrational. His behavior makes sense if you consider the effects of confirmation bias. Santorum believes that the President is trying to indoctrinate college students to become liberals. He believes it so thoroughly that he simply filters out any evidence that would contradict it. While most observers can hear the President say “one year of higher education or career training“, Santorum doesn’t. He hears the part confirms his beliefs and filters out the rest. I’d imagine that for Santorum, listening to President Obama speak sounds something like the teacher from the Peanuts cartoons: “one year of higher education wah wah-wah wah-wah-wah“. To Santorum’s credit, at least he had the mind to retract his “snob” statement — even if only partially. This shows that the underlying mechanisms for rational behavior are still there, despite his frequent leaps of logic.

Conclusion

I hope I’ve at least managed to present a definition of “rationality” that’s a little more precise than the everyday use of the term. I’m sure some people out there might disagree with the way I’ve rated the “rationality” of these behaviors. Different people have different experiences and consequently have different assumptions about the world. If we were to use multiple “rationality raters” and average the results, perhaps we might have a decent quantitative measure of rationality to work with.

Part of the problem with measuring rationality is the speculative nature of trying to determine someone else’s assumptions. We can generally use what a person says as an indication of what they believe — at least for the most part. It’s also important to consider not only the statement, but the context in which the statement is made. In political discourse, we implicitly assume that politicians are being honest with us. They might be wrong about the facts, but this idea that they are honestly representing their own views is something that voters tend to select for. Perhaps this is why Romney is still struggling against Santorum in the primary. Santorum may have problems getting his facts straight and presenting a logical argument, but he has a habit of saying what he believes regardless of the consequences. Romney, on the other hand, says what he thinks will win him the most votes. Many voters do not vote “rationally”, they vote according to how they “feel” about the candidates. Romney may be more “rational” than Santorum, but his calculated responses cause him to lose that “feeling of honesty” that Santorum elicits from voters.

In the next article, I’ll attempt to explain the origins of rational and irrational behavior. I think the key to understanding these behaviors lies in evolution by natural selection. I would argue that both rational and irrational behaviors contributed to the survival of our species, and this is why irrationality persists into the present. Stay tuned!

Posted on
by

I’m a long time fan of the Final Fantasy series, going back FF1 on the NES. In fact, I often cite FF4 (FF2 US) as my favorite game of all time. I enjoyed it so much that it inspired me to learn how to program! One of my earliest Java applets was based on a Final Fantasy game and now, 15 years later, I’m at it again.
I had a blast playing FF13, so when I heard about its sequel I had to pick it up. The game is fun and all, but I’ve become slightly obsessed with a particular minigame: The Clock Paradox.

The rules of the game are simple. You are presented with a “clock” with some number of buttons around it. Each of these buttons is labeled with a number. Stepping on any of the buttons deactivates that button and moves the two hands of the clock to positions that are the distance away from that button specified by the labeled number. After activating your first button, you can only activate the buttons which are pointed at by the hands of the clock. Your goal is to deactivate all of the buttons on the clock. If both hands of the clock point to deactivated buttons and active buttons still remain, then you lose and must start over.
See this minigame in action in the video below:


You may not know this about me, but I’m not a real big fan of manual “guess and check”. I would rather spend several hours building a model of the clock problem and implementing a depth first search to find the solution, than spend the 5 minutes of game time trying different combinations until I find one that works. Yes, I’m completely serious. Here it is.
I think that the reason why I’m drawn to this problem is that it bears a close relation to one of the Millennial Problems: P vs NP. In particular, the Clock Paradox is a special case of the Hamiltonian Path Problem on a directed graph (or digraph). We can turn the Clock Paradox into a digraph with the following construction: create a starting vertex, draw arcs to each position on the clock and place a vertex, and finally draw two arcs from each positions following the potential clock hands from that position. The Hamiltonian path is a sequence of arcs that will visit each vertex exactly one. If such a path exists, then the Clock Paradox is solvable.

This little minigame raises several serious mathematical questions:

  • What percentage of the possible Clock Paradoxes are solvable?
  • Is there a faster method of solving the Clock Paradox? Can it be done in polynomial time, or is it strictly exponential?
  • Is there any practical advise topology can offer to help players solve these puzzles?
  • Is there anything these puzzles can teach us about the general Hamiltonian Path Problem?

I don’t claim to know the answers, but I would offer the following advise: see if you can identify a node with only one way in or out. If you can, then you know that you’ll need to start or end. If all else fails, you can always cheat by plugging it into my sim!
That’s all I have for today. Maybe there will be some rigged chocobo races in the future… kupo.

Posted on
by

I find it rather interesting that the foundations of both logic and democracy can be traced back to ancient Greece. Here in the US, we’ve taken the Greeks’ idea of democracy and brought it to a new level, but at the same time our political discourse seems anything but logical. We owe to Aristotle the “Three classic laws of thought”, which are as follows:

  1. The law of identity. Anything object must be the same as itself. $$ P \to P $$
  2. The law of noncontradiction. Something can’t be and not be at the same time. $$ \neg(P \land \neg P) $$
  3. The law of excluded middle. Either a proposition is true, or it’s negation is. $$ P \lor \neg P $$

It’s worth while to note that these statements are neither verifiable or falsifiable, qualities true of any “axiom”. An axiom is supposed to be a self-evident truth, that gives us starting point for a discussion. The universe described by these axioms is one where “TRUE” and “FALSE” form a dichotomy. These axioms don’t handle things like quantum particles or Russell’s paradox in which things can be both true and false simultaneously. Nevertheless, they provide a useful tool for discerning truthhood. Politicians, however, are more concerned with “votes” than “truths”. The following “Three Axioms of Political Alogic” are the negation of the “three classic laws of thought”, and generally indicate situations where a politician is distorting the truth for personal gain. Although, that could change if Schrodinger’s Cat decides to run for office.

The Three Axioms of Political Alogic

#1: The law of deniability

Just because something is, doesn’t mean that it is.
First order (a)logic: $$ \neg (P \to P) $$
Sometimes politicians don’t have their facts straight, but that won’t stop them from proclaiming that a lie is the truth. The most common form of this seems to be the denial of evolution and climate change, despite the overwhelming scientific evidence. When the majority of the population is poorly informed about scientific issues, its much easier for a politician to appeal to these voters by reaffirming their misconceptions than it is to actually educate them. Just ask Rick Santorum.
There’s a corallary to this rule, and that is that if you repeat the lie often enough then eventually the public will believe you. The right-wing media repeatedly refers to President Obama as “Socialist” or “Muslim”, despite neither being true, in the hopes of eventually convincing the public that they are true.

#2: The law of contradiction

Just because two positions contradict each other, doesn’t mean you can’t hold both of them simulatenously.
First order (a)logic: $$ P \land \neg P $$
Politicians seem to have a natural immunity to cognitive dissonance, allowing them to hold two contradictory positions without feeling any guilt or embarrassment. Republicans like to call themselves “pro-life” while simultaneously supporting the death penalty — something I never fully understood. How can one be pro-life and pro-death at the same time?
President Obama’s 2012 State of the Union had a few subtle contradictions worth noting. President Obama begins by praising the General Motors bailout and goes on to speak out against bailouts near the end. He also called out “the corrosive influence of money in politics”, while he himself was the largest beneficiary of Wall St donations during the 2008 campaign. When you consider that this President has built his position on the principles of compromise and cooperation, taking both sides of the issue seems to be his way of encouraging both parties to work together. Unfortunately, this strategy hasn’t really worked out that well in the past.

#3: The law of the included middle

You don’t need to choose between a position and its negation. You can always change your mind later.
First order (a)logic: $$ \neg (P \lor \neg P) $$
Politicians try to appeal to the widest possible base of voters. Since the voters don’t always agree with each other on a particular issue, you’ll often find politicians changing their stance depending on which voters they’re speaking to. This law is the “flip-flop” rule of politics. Mitt Romney is a popular example, having changed his stances on abortion, Reaganomics, and no-tax pledges. These changes make sense from a vote-maximization point of view. Romney’s earlier campaign in Massachusetts required him to appeal to a moderate voter base. In the GOP Primary, he now needs to contend with the far-right wing voters. If the votes he potentially gains by changing stance outnumber the votes he’d lose from the flip-flop, then he gains votes overall. Likewise, President Obama has also “flip-flopped” on some issues he campaigned on now that he’s actually in office — like single-payer healthcare versus individual mandates. Again, the President is dealing with a change in audience. “Candidate Obama” needed to appeal to the general population, while “President Obama” needs to appeal to members congress. He’s still trying to maximize votes, it’s just a different type of vote that counts now.

Parting Thoughts

This post started with a joke on Twitter about politicians’ inability to do basic math or logic. After giving it some thought, perhaps they’re better at math than I originally gave them credit for. They may not be able to answer simple arithmetic problems, but when it comes down to maximizing the number of votes they receive they are actually quite skilled. They may tell bold faced lies and flip-flop all over the place, but they do so in such a way that gets them elected and keeps them there. If we want politicians to tell the “truth” then we to start voting that way. We also need to start educating others about how to tell a “lie” from the “truth”, and I hope someone finds these “Three Axioms of Political Alogic” a valuable tool for doing so.

Posted on
by

Last Thursday’s #mathchat topic was “Is the spirit of mathematical thinking being swamped by a focus on technique?”. One of the things that caught my eye during this discussion was a comment by David Wees suggesting that we teach math more like programming. I’ve proposed something similar to this before, but as the conversation continued into the details of learning how to program I started to think of the process like learning a foreign language. While I quickly came to realize that there were differing views on how foreign languages should be taught, I think there might be something to this idea. The human brain has built-in hardware to assist in learning language. Can math education take advantage of it?

Mathematics has its something of its own written language. A “conventional mathematical notation” has emerged through a variety of social influences. Some of those notations “just make sense” in the context, while others are adopted for purely historical reasons. As an undergraduate, college mathematics was like learning a foreign language for me. I had no idea what “$$ \forall n \in \mathbb{R} $$” meant. Aside from “n“, those symbols were not used once in any of my previous courses! It was culture shock. I eventually adjusted, but I now understand why mathematical notation can have such an intimidating effect on people.

What follows are my experiences with learning two foreign languages and how I think the difference between the two methodologies relates to the “math wars”. I had 2 years of Spanish in high school and 3 semesters of Russian in college. I’m going to refer to the teachers as Mrs. T and Mrs. R respectively, for reasons that I think will be obvious later.

Mrs. T’s Spanish class was held in a portable classroom at the edge of the high school. The classroom held about 30 students and the air conditioning barely kept out the 100-120 degree desert heat. I must give Mrs. T some credit for being able to do her job under such conditions. The classes often started with practice reciting words and phrases, followed by worksheets in groups and ending in a quiz. “Capitones, vengan aqui”, she would say while slamming her hand down on the table in front of her, indicating that the students in the front row of the class were to carry everyone’s work up to her. Everyday she would do the same routine, and everyday I wished that table would snap in half. We had done so many 10 point worksheets that at the end of the semester I came to the mathematical conclusion that the 100 point Final was only 2% of my grade. Being the little smart-ass that I was, I pointed out that I could skip the Final and still get an A. I don’t think she liked that very much, because she threatened to fail me if I didn’t take it. Aye que pena!

Mrs. R’s class was much smaller, with only about 8 students. It was more like a conference room than a classroom. There was a U-shaped table that opened towards the white board, so Mrs. R could walk up to each person and engage in conversation. There was some rote memorization at first, while we learned the alphabet and basic grammar, but after the first few weeks of class Mrs. R started refusing to speak English in class. Class started with everyone saying hello and talking about his/her day — in Russian. We role-played different situations — in Russian. If I needed to know a word, I had to ask about it — in Russian — and someone would explain it to me — in Russian. We watched Russian films and listened to Russian rock music. It didn’t feel like a class, but rather like 9 friends with similar interests hanging out for an hour each day.

In both of the classes I learned much about the respective languages, but what really stuck with me in each case was the culture. I might not remember enough of the vocabulary to consider myself fluent in either language, but I’ll still find myself singing along with Santana or Mashina Vremeni.

In the “Math Wars”, the Traditionalists follow something similar to Mrs. T’s method while the Reformers want math to look more like Mrs. R’s class. Both methods “work”, if test scores are all you care about, but there’s a very subtle difference between them. In Spanish class, I always felt like I was always translating to and from English in order to communicate. In Russian class, I felt like I was articulating ideas directly in Russian. There’s something beautiful about just immersing yourself in a different language until you learn it. I learned how to program in C by installing GNU/Linux and reading other peoples’ source code. Sure I read a few books on the matter, but it was immersing myself in “C culture” that really solidified my understanding.

For students to really learn math, they need to be immersed in the “culture of mathematical thinking”. I might not agree with the term “spirit”, but mathematicians seem to display a common pattern of asking very entertaining “what if?”s and seeking out the answers. You can find beautiful math in something as simple as drawing doodles in class. There’s more mathematical thinking going on when two kids make up a game during recess than there is in a thousand worksheets. Our body of mathematical knowledge is formed through communication and peer-review. It’s is such a shame to see math classes run like a dictatorship, built around memorizing a list of “techniques”. Sure, mathematics is an essential skill in finance, data, and engineering, but lets not underestimate the importance of “asking questions” in our focus on “problem solving”.

Proceeding with the question “what if we teach math like a foreign language?”, what might we do differently?

Mrs. T might argue that repetition seems to work, and there’s a substancial amount of evidence it does (at least in the short term). Math class already has its fair share of repetitious worksheets, but what if we shift the focus of the repetition to learning the “alphabet and grammar” of mathematics earlier like Mrs. R’s class? We could start with “set theory” and “logic” then work up from a firm foundation. The benefits could be substantial.

Mrs. R might also argue that students need to be immersed in the culture of math. Students should learn about the history of math and be exposed to “mathematical pop culture”. Let’s laugh together at XKCD or collectively gasp in bewilderment at the arXiv. It’s moments like those that make us human. Lets embrace them.

Embrace the “culture of math”.

Of course, it would probably be a lot easier to do such a thing with a student-teacher ratio of 8:1. One can only dream…

Posted on
by

Last year, I wrote an article about Street Fighter and Game Theory for Mathematics Awareness month. This year, the theme is “Unraveling Complex Systems” and I thought I would take the opportunity to expand on the mathematics of fighting games. Lately I’ve been playing a lot of Marvel vs Capcom 3, and in this article I’m going to attempt to show how the online community in MvC3 is a complex system. This article is intended for casual video gamers, but the mathematically curious might enjoy playing with included sample code. The sample code has been written in Scheme using Racket, formerly known as Dr. Scheme.

Marvel vs Capcom 3 and Rock, Paper, Scissors

In my last article, I made the case that fighting games in general can be thought of as a game of “Rock, Paper, Scissors”. In Marvel vs. Capcom 3, there are several different levels of “Rock, Paper, Scissors” going on within a single match. In addition to the “High, Low, Overhead” game discussed in my previous article, we also have games like “Attack, Block, Throw” and “Jump-in, Anti-Air, Projectile”. You can even see something of a “Rock, Paper, Scissors” game going on between different characters. What makes MvC3 different from other games in the fighting genre is that you have a roster of three characters playing simultaneously. This makes between individual character differences less important in the larger scheme of things, but what is more important is the strategy behind those three characters.

In MvC3, there are three basic strategies: “rush-down”, “keep-away”, and “turtle”. The “rush-down” strategy is simple, get up close to the opponent and attempt to dish out as much damage as possible. Some characters lend themselves to this strategy more than others, with a few notable ones being Wesker and Wolverine. The idea behind “keep-away” is to control the distance between you and your opponent using ranged attacks and projectiles. Some characters with a good keep-away game include Storm and Sentinel. The last strategy is “turtling”, which is playing a defensive game while waiting for an opportunity to punish a mistake from the opponent. Characters like Haggar and Hulk can make short work of an opponent once the right opportunity arises. While “turtling” can be highly effective against “rush-down” tactics, it tends to not do well against “keep-away” tactics. Thus, “rush-down” beats “keep-away”, “keep-away” beats “turtle”, and “turtle” beats “rush-down” – completing our game of “Rock, Paper, Scissors”. The pay-off matrix for this model might look something like this:

  Rush-Down Keep-Away Turtle
Rush-Down (0,0) (10,0) (0,10)
Keep-Away (0,10) (0,0) (10,0)
Turtle (10,0) (0,10) (0,0)

Consider a match-up between characters like Wolverine and Storm. Wolverine’s set of moves might complement a rush-down approach while Storm’s set of moves complement a keep-away strategy. The player playing Storm would likely attempt to “keep-away” from Wolverine as long as possible, chipping away at his health via block damage. Essentially, Wolverine has forced into a “turtle” position while the distance between the two is large because he doesn’t have the tools to attack from afar. Wolverine’s “rush-down” game doesn’t start until he closes the distance between them. Once Wolverine is in close, it’s going to be hard for Storm to shake him. Storm would need to switch into a “turtle” strategy until she can find an opening between the oncoming attacks to create some distance again.

Keep in mind that these are strategies, and not dispositions of particular character. While some characters in MvC3 may lend themselves to a certain strategy over others, you have three characters to choose from and all of them can be played in any of these three styles to some extent. A individual character’s weaknesses can be compensated for with the appropriate assists. For example, the Wolverine player might choose a partner like Magneto with a beam-assist to help with his ranged game and the Storm player might choose a defensive assist like Haggar to help counter rush-down tactics.

In a given game of MvC3, it’s important to be able to change strategies on the fly. You might start the match with a “rush-down” approach, change to “keep-away” when the opponent starts “turtling”, then go back to a “rush-down” to finish off the match. Abstractly, we can look at MvC3 as a mixed strategy by assigning a probability to each of these three play styles. For example, lets consider two players in a hypothetical match. Player 1 chooses a rush-down heavy team mixed with a little turtling — lets say 80% rush down, 0% keep away, and 20% turtling. Player 2 chooses a well balanced team, but leaning slightly towards the keep-away game – 30% rush-down, 40% keep-away, and 30% turtling. We can multiply these strategies with our pay-off matrix to find the expected outcome. In this case, the average pay-off is 3.8 for player 1 and 3.2 for player 2. Over the long run, we might expect player 1 to win roughly 54% of the time. By specializing in one strategy at the expense of others, player 1 has gained a slight advantage over player 2. However, player 1’s strategy could also be foiled by a player that has chosen to focus on “turtling”. Consider a third player with a strategy of 0% rush-down, 40% keep-away, and 60% turtle. This player would have a 5.6 to 3.2 advantage over player 1, but be at a slight disadvantage to player two by a rate of 3 to 3.6.

Metagaming

In the example above, we’ve seen how it’s possible to adjust strategies to gain an advantage over a particular opponent. In the event that you know nothing about your opponent’s strategy, your best bet (from a mathematical standpoint) is to play each strategy with equal probability. However, the pay-off from this particular strategy is that you’ll break even – win 1/3 of the matches, lose 1/3 of the matches and tie 1/3 of the matches. In order to win with any consistency, it is necessary to predict which strategy your opponent will play. This is where metagaming comes in.

Metagaming is the art of stepping outside of the game and using information external to the game rules to optimize the potential pay-off. In MvC3, we might examine the frequency with which each character is played and keep track of trends in player strategy. If the majority of the population is predominantly playing one strategy, then it’s possible build a counter-strategy that will result in a favorable outcome. For example, Sentinel tends to emerge as a high-frequency character in MvC3 online matches. Sentinel’s strong keep-away game (high beam, low beam, rinse & repeat) tends to shutdown a large number of beginning players. In order to win against Sentinel, it’s necessary to be able to close that distance and rush him down. A character like Wesker might be particularly well suited for this role.

The metagame of MvC3 is constantly changing. As new strategies become dominant, new counter strategies emerge. On occasion, one of these new counter strategies will become dominant and new counter strategies will will start to develop. Each individual player is an autonomous agent. That player makes his/her own decisions about how to play. However, this player is not alone and may face a diverse range of opponents, each with their own individual strategies. Depending on what types of opponents a player faces, that player can learn from those matches and adapt a new strategy when appropriate.

From a mathematical standpoint, the metagame in MvC3 is essentially a “complex system”. We have a network of independent players connected together by matches played online. The game itself is highly structured with a fixed set of rules, but when we look at the system as a whole it can exhibit a variety of unexpected behaviors. To look at this system from a mathematical viewpoint, we might take a modeling approach. We set up a simple model of the system, add some players and connections between them, then let the model run and see what kinds of properties emerge.

Genetic Algorithms

One way that we might model this system is by using a genetic algorithm. A genetic algorithm is a programming paradigm based on evolution by natural selection. Natural selection dictates that the organisms that are best fitted for survival in a population are the ones that live to reproduce and pass their genes on to a new generation. In the context of this particular system, our environment is a population of players with varying strategies. Instead of genes, we have strategies employed by those players. If a player’s strategy works relatively well against the population, that player will likely continue to use it. If a strategy doesn’t work, it’s back to training for a new one.

With this basic genetic algorithm, let’s see what happens when we start with a small group of 5 players each playing a perfectly balanced game (1/3, 1/3, 1/3). After each play-off, the top 4 players keep their existing strategies and the loser goes back to the drawing board and chooses a new strategy at random. As we look at the changes in strategy over time, we can see that the top 4 players stay the same, generation after generation. We say that (1/3, 1/3, 1/3) is an “evolutionarily stable strategy”. As long as the majority of the population plays this strategy, no new strategy can take over the population. In gaming, this is not really a desirable thing to happen. The game isn’t fun when every plays the same thing, and players generally refer to this as a “stale metagame”. It really shouldn’t be that surprising that the system behaves like this, considering that (1/3, 1/3, 1/3) is the mathematically optimal strategy for this particular payoff matrix.

One of the interesting things about complex systems, is that you often see a high sensitivity to initial conditions. If we make a small change to the initial strategies in the previous example, say (.34, .33, .33) instead of (1/3, 1/3, 1/3), this increases the likeliness of a new strategy to infiltrate that elusive top four. There’s an element of randomness as to when the new strategy will succeed, it could happen after the first generation or after the hundredth. Once it does, it starts to change the environment which allows other new strategies to succeed as well. In some sample runs of this population, only one or two of the original strategies were left after 10,000 generations – but there’s a great deal of variance between trials. Playing a well balanced game is often a key feature of the new strategies, but might start to see a slight shift from “rush-down” to “turtle” emerging over time, countering the initial population’s slight bias toward this strategy.

When MvC3 first came out, the metagame was largely dominated by a single character: Sentinel. Upon observing this, Capcom issued a patch reducing Sentinel’s health. Some players criticized Capcom for this move, because it didn’t change the gameplay mechanics that were being abused, but from our example here we can see how a small change can have large effects on the metagame. Overall, I think this was a pretty smart move by Capcom – it was just enough change to make the metagame interesting again.

The previous two examples have dealt with small populations that are mostly uniform to start with. In the real world of MvC3 online play, there are thousands of players with dramatically different strategies to start with. To attempt to model the MvC3 metagame, we need to look at larger player pools with a greater diversity of play-styles. To get a feel for this, let’s look at a population of 20 random strategies, and replace the bottom 5 players with new strategies each round. With these changes, we see much more variance in the top players.

From one sample run with these conditions:

  • The top strategy after the first generation was (0.54, 0.27, 0.19).
  • The top strategy after 10 generations was (0.13, 0.81, 0.06).
  • The top strategy after 100 generations was (0.69, 0.06, 0.24).
  • The top strategy after 1,000 generations was (0.04, 0.81, 0.15).

There are many interesting observations to be made about the behavior of this model. First, we see that the metagame is much more dynamic when we start with random conditions instead of a uniform population. Balanced strategies tend to do well overall, but many of the top strategies are not necessarily balanced. Remember, its not the strategy alone that determines success, but the combination of the strategy and population. The fact that the top strategies after 10 and 1,000 generations are both “keep-away” heavy is a result of the population being “turtle” heavy during those particular generations. As the population changes, so do the winning strategies change. This ebb and flow from one strategy to another is what keeps the metagame interesting.

Conclusions

I think there’s a couple of important lessons to be learned here for people who are new to the fighting game genre. The first lesson is the importance of a balanced game. If everyone is playing a balanced game, then the only way to be successful to play a balanced game. The second lesson is to not underestimate “gimmick builds” – strategies that focus on maximizing a particular play style at the expense of other. When there is a tendency for the general population to play a certain way, the right counter strategy can be highly effective. The third lesson is to learn from your mistakes. If your team strategy isn’t working, don’t be afraid to mix it up. You might find a new strategy works better against the general population.

As a footnote, I’d like to point out that this model is a very simplified version of what goes on in MvC3 games. For an example of what some “real” MvC3 games look like, I’d recommend having a look at Andre vs Marn’s First to Ten. As you watch, see if you can identify when each player is playing which strategy. Does the rush-down/keep-away/turtle model fit with actual fights? How does changing out Akuma for Sentinel change Marn’s strategy? Is this change predicted by our model?

Further Investigations

I’ve intentionally been a little vague with the definition of complex system, in part because most definitions are high level descriptions of behavior. Am I correct in the assertion that MvC3 single player is not a complex system, but the MvC3 multiplayer “metagame” is a complex system?

One of the things I find interesting about MvC is the assist system. In this system, its technically possible for a player to employ two different strategies simultaneously. How can we change our model to account for this?

One common practice for genetic algorithms is to mix the genes of successful players to create new players, rather than just randomly selecting a new strategy as done in this example. Typically this is done by using a “crossover”, which selects randomly selects genes from two parents. How does this change the results of the genetic algorithm?

Another way of looking at the players is to actually model each player as a program. This technique is often called genetic programming. What kind of programs do you think would be most successful?

Further Reading

Gintas, H. (2000). Game Theory Evolving. Princeton University Press: Princeton.

Mitchell, M. (1998). An Introduction to Genetic Algorithms. MIT Press: Boston.

Koza, J. (1980). Genetic programming: on the programming of computers by means of natural selection. MIT Press: Boston.

Dawkins, R. (1976). The Selfish Gene. Oxford University Press: Oxford.

Felleisen, M., Findler, R., Flat, M. & Krishnamurthi, S. (2003). How to Design Programs. MIT Press: Boston. Available online at HTDP.ORG.

Posted on
by

Last weekend I attended the 25th Annual Conference of The Virginia Mathematical Association of Two Year Colleges (VMATYC), Virginia’s chapter of the American Mathematical Association of Two Year Colleges (AMATYC). This was the first educational conference I have been to since I started teaching developmental math two and half years ago, so it was a very exciting event for me. What follows is my account of the seminars I attended at the VMATYC and what I learned from the experience. I’ve tried my best to summarize the events I attended from my notes, but please contact me if there are any inaccuracies.

I missed the early sessions on Friday due to class, but made it in time for the seminar I was most interested in: The Developmental Math Redesign Team (DMRT) Progress Report.

DMRT Progress Report

Virginia’s Community College System (VCCS) has been in the process of “redesigning” the developmental math program for about two years now, and is now in the process of implementing some major changes to the way developmental math is handled at the community college level. The report was presented by Dr. Susan Wood, Dr. Donna Jovanovich, and Jane Serbousek.

Dr. Susan Wood began the discussion with a broad overview of the DMRT program. The DMRT began in 2009 with the publication of The Turning Point: Developmental Education in Virginia’s Community Colleges, which highlighted some of the problems facing developmental math students. This document set forward the goal for the developmental education redesign, which is specifically targeted at increasing the number of students that go on to complete degree programs. The Turning Point also initiated the Developmental Mathematics Redesign Team. The following year, the DMRT published The Critical Point: Redesign Developmental Mathematics Education in Virginia’s Community College System, which outlines the proposed changes to the developmental education program. Next, a curriculum committee began work on a new developmental mathematics curriculum, which is available here. These changes are slated for implementation in Fall 2011. Dr. Wood also made the point that these changes fit into a larger framework of the student experience, a cycle of “Placement/Diagnostic Instruments –> Content –> Structure –> Instructional Delivery –> Professional Development –> Student Support Services Assessment –> Placement/Diagnostic Instruments”.

Next, Jane Serbousek followed with more detail about the proposed DMRT changes. The content of the developmental math courses has been revised to better reflect what is needed to be successful in college. The content has also been reorganized from three five-unit courses, to a series of nine one-unit “modules”. The modules are competency based, and are intended to use a grading system of ABCF instead of SRU (Satisfactory, Reenroll, Unsatisfactory) which is currently employed. She noted that the question of “what constitutes mastery?”, is a difficult one. The intention of this modular framework is that students should only take the modules that are needed, as determined by the placement test, and work to improve their mastery of that topic before moving forward. This also allows for greater differentiation between students. For example, Liberal Arts students would have different developmental math requirements than students in STEM programs.

Part three of the presentation was led by Dr. Donna Jovanovich and discussed the goals of developmental math redesign. The three goals of the DMRT are (1) to reduce the need for developmental education, (2) reduce time to complete developmental education, and (3) to increase number of developmental education students graduating or transferring. Each of these goals has a related measure of success. For example, “reduced need for developmental education” can be measured by placement test scores and “reduced time to complete developmental education” can be measured by student success in developmental classes. One interesting statistic that Dr. Jovanovich mentioned was the following: only 1/3 of developmental math students that don’t pass reenroll in the course the following semester, of those, only 1/3 pass the second time, but those that do pass through the developmental program successfully have a 80% of graduating or transferring. So while success rates for the courses are grim, there are long term payoffs for the students who do succeed.

Dr. Wood returned at the end of the session for some closing remarks. The steps for the DMRT program are to have the curriculum approved by the Dean’s course committee and to find out how the modularization of developmental math will affect enrollment services and financial aid.

For more information, see the VCCS Developmental Education home page.

VCCS Reengineering Initiative

The second event I attended was a presentation from VCCS Chancellor, Dr. Glenn DuBois. The Chancellor began with an overview of the goals for the Reengineering Initiative, many of which are spelled out in the Achieve 2015 publication. The goals are to improve access, affordability, student success, workforce and resources. He noted that the VCCS is experiencing an increased number of students that register for classes, and increased number of these students are unprepared, a decrease amount of public funding, along with a call for more public accountability and more college graduates. Currently, about 50% of high school graduates require developmental education and only 25% of them go on to graduate in four years. He made the case that there is bipartisan support for improving the quality of education, using President Obama and Virgina Governor McDonnell as two examples. President Obama has stated that he wants to see 5 million more graduates in the US, while Governor McDonnell has stated that he wants to see 100,000 more graduates in the state of Virginia. This is the heart of the Reengineering Initiative: improving student success with sustainable and scalable solutions. Some of the funding for the Reengineering Initiative has been made possible by Federal funding, as well as the Lumina & Gates foundations.

In order to improve the 25% success rate of developmental education, the Reengineering Initiative is implementing major changes to the developmental math program. First is the opening of different paths for different students. Second is a revised business model which replaces a “test in/test out” philosophy with a diagnostics and short modules intended to improve mastery. To accomplish these goals, the Virginia Community Colleges are moving in a direction of more shared services, in areas such as Financial Aid and distance learning. The VCCS is also looking for ways to help local high schools better prepare students for college, such as making the placement test available to high school students and developing transition courses.

Best Practices in a Changing Developmental Education Classroom

The last event of the first day was a keynote presentation from textbook author Elayn Martin-Gay. Elayn’s first major point was about the importance of “ownership” for both teachers and students, and how language can affect the feeling of “ownership”. For example, instead students’ grades being “given”, they should be “earned”. She seemed very positive about the Reengineering Initiative, saying that it was “good to be doing something, even if it’s wrong, [so that] you can tweak it and continue”.

She then proceeded into more classroom oriented practices, saying that it was important to monitor student performance and catch students “at the dip”. If a drop in performance can be corrected early, this can prevent the student from getting too far behind. She also talked about the importance of students keeping notes in a “journal”. This encourages good study skills, giving students a source to go to when it comes time for the exam. She suggested that teachers should “learn the beauty of a little bit of silence”. Teachers should not always jump right into a solution to a problem, but that waiting a extra three seconds longer will dramatically increase the number of student responses. She also said that teachers should “raise the bar and expect more from students”, and that “they will rise to meet it”. She recommended that disciplinary problems occurring in the classroom should be taken care of immediately, to maximize time for learning later.

After these classroom practices, she moved into some of the larger social issues affecting developmental education. She noted that the supply of college degrees has gone down, while the demand for experts has gone up. She jokingly called the first year of college “grade 13”, noting that many college freshmen have yet to decide on a long term plan. She cited seven current issues affected new college students: lack of organization, confidence, study skills, attendance, motivation, work ethic, and reading skills. She argued that reading is often the biggest barrier to earning a college degree.

As some ways of addressing these issues, she presented a number of graphs relating college experience with employment and income. She said that she often presents these graphs at the start of the semester as a means of encouragement. She has students covert the statistics from annual income to an hourly wage so that they can more closely relate with the figures. She also included some ideas for asking “deeper” questions in math classes. One of the examples was “Write a linear equation that has 4 as the solution”. The trivial solution to this is “x=4”, then we can build off this to find others “2x=8” and “2x-3 = 5”. She says that students will typically solve these equations step by step each time, by the time she asks students to solve something like “-2(2x-3)/1000 = -10/1000” they start to look for an easier method – realizing deeper properties about equality in the process.

One of the things Elayn said that resonated strongly with me was that “students would rather be in charge of their own failure than take a chance on [asking the teacher]”. As math teachers, the general feeling of the audience was that study skills are not our focus, but as Elayn pointed out, those study skills can have a powerful influence on student success. By providing students with the skills necessary to “learn math”, those students can in turn take charge of their learning experience.

Next time: VMATYC Day 2

Stay tuned as I collect my notes from Day 2. Day 2 events include: “Online Developmental Math on the Brink: Discussion Panel”, “Developmental Mathematics SIG Roundtable”, and “The Mathematical Mysteries of Music”.